Question

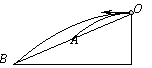
【题目】如图所示，水平光滑地面上停放着一辆质量为M=2kg的小车，小车左端靠在竖直墙壁上，其左侧半径为R=5m的四分之一圆弧轨道AB是光滑的，轨道最低点B与水平轨道BC相切相连，水平轨道BC长为3m，物块与水平轨道BC间的摩擦因素μ=0.4，整个轨道处于同一竖直平面内．现将质量为m=1kg的物块（可视为质点）从A点无初速度释放，取重力加速度为g=10m/s2.求：

(1)物块下滑过程中到达B点的速度大小；

(2)若物块最终从C端离开小车，则此过程中产生的热量；

(3)为使小车最终获得的动能最大，求物块释放点与A点的高度差．

Answer 1

【答案】（1）10m/s　（2）12J　（3）3.2m．

【解析】

(1)物块由A到B，根据动能定理求出物块下滑到B点的速度大小.(2)产生的热量等于滑动摩擦力与相对位移的乘积．结合Q=μmg△x求出产生的热量.(3)作出小车和物块的速度时间图线，分析何时小车的动能最大，结合运动学公式和动能定理求出物块释放点与A点的高度差.

(1)从A到B，由动能定理得：

可得：v0=10m/s

(2)从B到C，此过程中相对位移为BC板长，产生的热量为：Q=μmgL=0.4×1×10×3J=12J

(3)分析可知：只有相对滑行阶段小车方可加速：且

对小车，由，知：只有t最大，小车最终获得动能才最大．

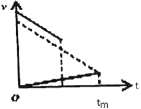
由v-t图象可知：物块滑到小车右端时恰好与小车共速即可．

设滑块到B点时速度为v，滑到右端时共同速度为v，小车加速时间为t，

则有：

得：t=1s，v=6m/s

设释放点与A点的高度差为△h，对滑块下滑阶段由动能定理得：

解得：△h=3.2m