题目内容
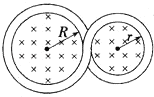
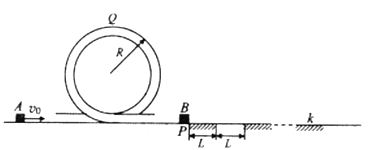
【题目】如图所示，半径为R=0.5m，内壁光滑的圆轨道竖直固定在水平地面上。圆轨道底端与地面相切，一可视为质点的物块A以
的速度从左侧入口向右滑入圆轨道，滑过最高点Q，从圆轨道右侧出口滑出后，与静止在地面上P点的可视为质点的物块B碰撞（碰撞时间极短），P点左侧地面光滑，右侧粗糙段和光滑段交替排列，每段长度均为L=0.1m，两物块碰后粘在一起做直线运动。已知两物块与各粗糙段间的动摩擦因数均为
，物块A、B的质量均为
，重力加速度g取
。
（1）求物块A到达Q点时的速度大小v和受到的弹力F；
（2）若两物块最终停止在第k个粗糙段上，求k的数值；
（3）求两物块滑至第n（n<k）个光滑段上的速度
与n的关系式。
【答案】（1）
，方向向下；（2）
（3）
【解析】（1）物块A滑入圆轨道到达Q的过程中机械能守恒，根据机械能守恒：
①
物块A做圆周运动：
②
由①②联立得：
方向向下 ③
（2）在与B碰撞前，系统机械能守恒，A和B在碰撞过程中动量守恒：
④
A、B碰后向右滑动，由动能定理得：
⑤
由④⑤联立得
，
所以
；
（3）碰后A、B滑至第n个光滑段上的速度
，由动能定理得：
⑥
解得：
练习册系列答案
相关题目
