题目内容
发射一月球探测器绕月球做匀速圆周运动,测得探测器在离月球表面高度分别为h1和h2的圆轨道上运动时,周期分别为T1和T2。设想月球可视为质量分布均匀的球体,万有引力常量为G。仅利用以上数据,可以计算出( )
| A.月球的质量 | B.探测器的质量 |
| C.月球的密度 | D.探测器在离月球表面高度为h1的圆轨道上运动时的加速度犬小 |
ACD
试题分析:根据万有引力提供向心力
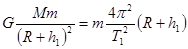 ,
,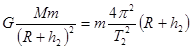 ,联立可求月舞的质量M、月球的半径R,再根据
,联立可求月舞的质量M、月球的半径R,再根据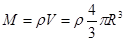 ,可求月球的密度,探测器的质量无法求出,探测器在离月球表面高度为h1的圆轨道上运动时的加速度
,可求月球的密度,探测器的质量无法求出,探测器在离月球表面高度为h1的圆轨道上运动时的加速度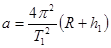 也可求出,所以A、C、D正确;B错误。
也可求出,所以A、C、D正确;B错误。
练习册系列答案
相关题目
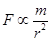 ,行星对太阳的引力
,行星对太阳的引力 ,其中M、m、r分别为太阳、行星质量和太阳与行星间的距离。下列说法正确的是
,其中M、m、r分别为太阳、行星质量和太阳与行星间的距离。下列说法正确的是
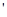 大小相等,是作用力与反作用力
大小相等,是作用力与反作用力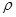 ;石油密度远小于
;石油密度远小于
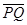 =x,利用“割补法”原理:如果将近地表的球形空腔填满密度为
=x,利用“割补法”原理:如果将近地表的球形空腔填满密度为 来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值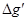 (
(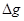 在OP方向上的分量)
在OP方向上的分量)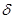 与
与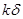 (k>1)(
(k>1)(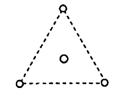

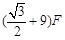
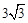 倍
倍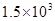 kg/m3的液态星球是否存在,他的主要根据之一就是它自转的周期,假若它存在,其自转周期的最小值约为( )(万有引力恒量G=6.67×10-11Nm2/kg2)
kg/m3的液态星球是否存在,他的主要根据之一就是它自转的周期,假若它存在,其自转周期的最小值约为( )(万有引力恒量G=6.67×10-11Nm2/kg2) ;
;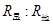 =1:2,求该星球的质量与地球质
=1:2,求该星球的质量与地球质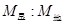 .
.