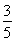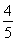题目内容
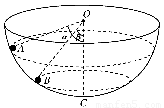
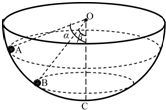如图所示，有一固定的且内壁光滑的半球面，球心为O，最低点为C，在其内壁上有两个质量相同的小球（可视为质点）A和B，在两个高度不同的水平面内做匀速圆周运动，A球的轨迹平面高于B球的轨迹平面，A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°，以最低点C所在的水平面为重力势能的参考平面，则（sin37°=| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
分析：小球受重力和支持力，靠两个力的合力提供向心力，根据平行四边形定则求出支持力之比，根据牛顿第二定律求出线速度和周期之比．
解答：解：A、根据平行四边形定则得，N=
，则
=
=
．故A正确．
B、根据mgtanθ=m
=mr(
)2，r=Rsinθ，解得v=
，T=2π
．则
=
，
=
．则动能之比为64：27．故B、C错误．
D、根据mgtanθ=m
得，动能EK=
mv2=
mgRsinθtanθ，重力势能EP=mgR（1-cosθ），则机械能E=mgR(1+
sinθtanθ-cosθ)，则
=
．故D正确．
故选AD．
| mg |
| cosθ |
| NA |
| NB |
| cos37° |
| cos53° |
| 4 |
| 3 |
B、根据mgtanθ=m
| v2 |
| r |
| 2π |
| T |
| gRsinθtanθ |
|
| vA |
| vB |
|
| TA |
| TB |
| ||
| 2 |
D、根据mgtanθ=m
| v2 |
| r |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| EA |
| EB |
| 112 |
| 51 |
故选AD．
点评：解决本题的关键搞清向心力的来源，运用牛顿第二定律得出线速度、周期的关系．知道机械能等于动能和势能的总和．
练习册系列答案
相关题目
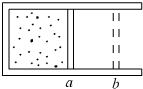如图所示，有一固定的圆筒形绝热容器，用绝热活塞密封一定质量的气体，当活塞处于位置a时，筒内气体压强等于外界大气压，当活塞在外力作用下由位置a移动到位置b的过程中，下列说法正确的是（ ）
（2008?内江二模）如图所示．有一固定的圆筒形绝热容器，用绝热活塞密封了一定质量的气体（气体分子间相互作用的引力和斥力均忽略不计）．当活塞处于位a时，筒内气体的压强等于外界的大气压强汽．当活塞在外力F的作用下由位置a移动到位置b的过程中，下列说法中正确的是（ ）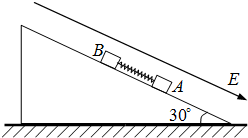
如图所示，有一固定的倾角为30°的斜面体，处在一个范围足够大的匀强电场中，电场线平行于斜面向下．斜面上放有两个物块A、B，质量分别为mA=0.8kg、mB=0.2kg，A带电，但B不带电，它们之间有一根用轻线拴住的压缩轻弹簧，弹簧与A相连，但与B不相连，弹簧的压缩量为30cm，具有的弹性势能为8.3J，A、B均处于静止状态．现突然剪断拴住弹簧的轻线，弹簧伸长并推动B沿斜面向上运动，直到B与弹簧分离，A、B在运动过程中始终没有离开斜面，一切摩擦都不计，并且A与斜面和弹簧的接触都是绝缘的，所带电荷量保持不变．（重力加速度g=10m/s2）
