题目内容
2.物体A放置在倾角为30°的足够长的光滑斜面底端O点,物体B放置在水平面上,A、B相距l=6m,现给A沿斜面向上的初速度v0=10m/s,同时给B水平向左的初速度v0′=8m/s,物体A、B与水平面之间的动摩擦因数μ=0.4,不考虑物体在O点的能量损失,求:(1)物体B运动到O点时,A距O点的距离;
(2)经过多长时间后A与B相遇.
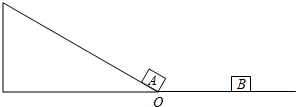
分析 (1)对B进行分析求出A、B的加速度,根据运动学公式求解B运动时间,再根据位移时间关系求解A位移;
(2)根据运动学公式分别列出位移时间关系,若相遇,则满足xB+X=xA解得相遇时间.
解答 解:(1)对B进行分析,B的加速度为:aB=μg=0.4×10=4m/s2
根据L=${v}_{B}t-\frac{1}{2}{a}_{B}{t}^{2}$
解得:t=1s
对A进行分析:aA=gsin30°=$10×\frac{1}{2}$=5m/s2
A的位移X=${v}_{A}t-\frac{1}{2}{a}_{A}{t}^{2}$
代入数值解得X=7.5m
故A距O点的距离为7.5m
(2)B在O点速度为v′B=v0′-aBt=8-4×1=4m/s
此时A的速度v${\;}_{A}^{′}$=v0-at=10-5×1=5m/s
到斜面上加速度与A相同为a=5m/s2,以沿斜面向上为正,
则xB=v${\;}_{B}^{′}$t′$-\frac{1}{2}a{t}^{′2}$①
xA=v${\;}_{A}^{′}$t′$-\frac{1}{2}at{′}^{2}$②
若相遇,则满足xB+X=xA③
联立①②③解得t′=7.5s
答:(1)物体B运动到O点时,A距O点的距离为7.5m;
(2)经过7.5s后A与B相遇.
点评 本题是追及相遇的题目,要对每个物体分别分析其运动情况,利用运动学的基本公式,再根据速度和位移的关系及牛顿第二定律求解.本题运动过程较为复杂,难度较大.

练习册系列答案
相关题目
12.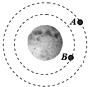 如图是我国于2011年9月29日发射的“天宫一号A”目标飞行器和11月1日发射的“神舟八号B”飞船交会对接前的轨道示意图.下列说法中正确的是( )
如图是我国于2011年9月29日发射的“天宫一号A”目标飞行器和11月1日发射的“神舟八号B”飞船交会对接前的轨道示意图.下列说法中正确的是( )
 如图是我国于2011年9月29日发射的“天宫一号A”目标飞行器和11月1日发射的“神舟八号B”飞船交会对接前的轨道示意图.下列说法中正确的是( )
如图是我国于2011年9月29日发射的“天宫一号A”目标飞行器和11月1日发射的“神舟八号B”飞船交会对接前的轨道示意图.下列说法中正确的是( )| A. | A和B的发射速度都应大于第二宇宙速度 | |
| B. | A的运行速率大于B的运行速率 | |
| C. | A的运行角速度小于B运行的角速度 | |
| D. | A的周期大于B的周期 |
13.在“5•12地震”后,灾区人民得了全国人民的大力帮助.灾后重建中,一辆运输建筑材料的汽车在水平路上匀速行驶时,输出功率还没有达到额定功率,进入上坡路段( )
| A. | 若保持速度不变,司机要加大油门增大输出功率,牵引力增大 | |
| B. | 若保持速度不变,司机要加大油门增大输出功率,牵引力不变 | |
| C. | 若保持输出功率不变,司机要用换档的办法减小速度,牵引力增大 | |
| D. | 若保持输出功率不变,司机要用换档的办法减小速度,牵引力不变 |
10.一质量为m的带电小球,在竖直方向的匀强电场中以水平速度抛出,小球的加速度大小为$\frac{2g}{3}$,空气阻力不计,小球在下落h的过程中,则( )
| A. | 小球的动能增加$\frac{mgh}{3}$ | B. | 小球的重力势能减少$\frac{2mgh}{3}$ | ||
| C. | 小球的电势能增加$\frac{mgh}{3}$ | D. | 小球的机械能减少$\frac{2mgh}{3}$ |
17.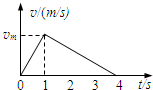 在水平公路上,汽车由静止开始做匀加速运动,当速度达到vm后立即关闭发动机,汽车滑行直至停止,其运动过程v-t图象如图所示,汽车牵引力大小为F,
在水平公路上,汽车由静止开始做匀加速运动,当速度达到vm后立即关闭发动机,汽车滑行直至停止,其运动过程v-t图象如图所示,汽车牵引力大小为F,
摩擦力为Ff,全过程牵引力做功为W,克服摩擦力做功为Wf,则( )
 在水平公路上,汽车由静止开始做匀加速运动,当速度达到vm后立即关闭发动机,汽车滑行直至停止,其运动过程v-t图象如图所示,汽车牵引力大小为F,
在水平公路上,汽车由静止开始做匀加速运动,当速度达到vm后立即关闭发动机,汽车滑行直至停止,其运动过程v-t图象如图所示,汽车牵引力大小为F,摩擦力为Ff,全过程牵引力做功为W,克服摩擦力做功为Wf,则( )
| A. | F:Ff=3:1 | B. | F:Ff=1:4 | C. | W:Wf=1:1 | D. | W:Wf=1:3 |
7.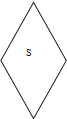 如图所示,在一个边长为l的菱形区域内,有垂直于纸面的匀强磁场,磁感应强度大小为B,菱形的一个锐角为60°.在菱形中心有一粒子源S,向纸面内各个方向发射速度大小相同的同种带电粒子,这些粒子电量为q、质量为m.如果要求菱形内的所有区域都能够有粒子到达,则下列粒子速度能够满足要求的有( )
如图所示,在一个边长为l的菱形区域内,有垂直于纸面的匀强磁场,磁感应强度大小为B,菱形的一个锐角为60°.在菱形中心有一粒子源S,向纸面内各个方向发射速度大小相同的同种带电粒子,这些粒子电量为q、质量为m.如果要求菱形内的所有区域都能够有粒子到达,则下列粒子速度能够满足要求的有( )
 如图所示,在一个边长为l的菱形区域内,有垂直于纸面的匀强磁场,磁感应强度大小为B,菱形的一个锐角为60°.在菱形中心有一粒子源S,向纸面内各个方向发射速度大小相同的同种带电粒子,这些粒子电量为q、质量为m.如果要求菱形内的所有区域都能够有粒子到达,则下列粒子速度能够满足要求的有( )
如图所示,在一个边长为l的菱形区域内,有垂直于纸面的匀强磁场,磁感应强度大小为B,菱形的一个锐角为60°.在菱形中心有一粒子源S,向纸面内各个方向发射速度大小相同的同种带电粒子,这些粒子电量为q、质量为m.如果要求菱形内的所有区域都能够有粒子到达,则下列粒子速度能够满足要求的有( )| A. | $\frac{\sqrt{3}Bql}{2m}$ | B. | $\frac{\sqrt{3}Bql}{6m}$ | C. | $\frac{Bql}{2m}$ | D. | $\frac{Bql}{m}$ |
11.关于地球的第一宇宙速度,下列说法正确的是( )
| A. | 它是人造地球卫星绕地球运行的最小速度 | |
| B. | 它是近地圆形轨道上人造地球卫星的运行速度 | |
| C. | 它是能使卫星进入近地轨道的最小速度 | |
| D. | 它是能使卫星进入近地轨道的最大速度 |
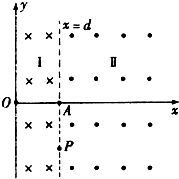 如图所示,在xOy直角坐标系内,0≤x≤d及x>d范围内存在垂直于xOy平面且等大反向的匀强磁场Ⅰ、Ⅱ,方向如图中所示,直线x=d与x轴交点为A.坐标原点O处存在粒子源,粒子源在xOy平面内向x>O区域的各个方向发射速度大小均为v0的同种粒子,粒子质量为m,电荷量为-q,其中沿+x方向射出的粒子,在磁场I中的运动轨迹与x=d相切于P(d,-d)点,不计粒子重力;
如图所示,在xOy直角坐标系内,0≤x≤d及x>d范围内存在垂直于xOy平面且等大反向的匀强磁场Ⅰ、Ⅱ,方向如图中所示,直线x=d与x轴交点为A.坐标原点O处存在粒子源,粒子源在xOy平面内向x>O区域的各个方向发射速度大小均为v0的同种粒子,粒子质量为m,电荷量为-q,其中沿+x方向射出的粒子,在磁场I中的运动轨迹与x=d相切于P(d,-d)点,不计粒子重力;