题目内容
【题目】如图所示,在倾角为θ的光滑物块P斜面上有两个用轻质弹簧相连的物块A、B;C为一垂直固定在斜面上的挡板.P、C总质量为M,A、B质量均为m,弹簧的劲度系数为k,系统静止于光滑水平面.现开始用一水平力F从零开始增大作用于P.(物块A一直没离开斜面,重力加速度为g)
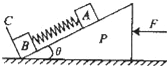
求:(1)物块B刚要离开C时力F.
(2)从开始到此时物块A相对于斜面的位移D.
【答案】(1)(M+2m)gtanθ(2)![]()
【解析】(1)物体B刚要离开C时,与挡板间的弹力为零,对AB以及弹簧整体分析如图:
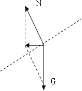
整体受重力和支持力,则整体的加速度a=2mgtanθ/2m=gtanθ
再对A. B. C.P整体分析,根据牛顿第二定律得:F=(M+2m)a=(M+2m)gtanθ;
(2)开始时,A处于平衡,有mgsinθ=kx,则弹簧的形变量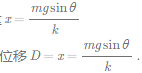 x=mgsinθ/k
x=mgsinθ/k
物块B刚要离开C时,弹簧处于原长,则A相对于斜面的位移D=x=mgsinθ/k。

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目