题目内容
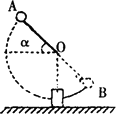
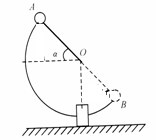
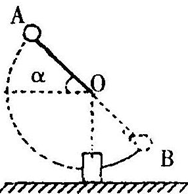
(15分)如图所示,摆锤的质量为M,摆杆长为L,其质量不计,摆杆初始位置OA与水平面成α角,释放后摆锤绕O轴无摩擦地做圆周运动,至最低点与质量为m的钢块发生碰撞,碰撞时间极短,碰后摆锤又继续右摆,刚好可以上升至B点,A、B、O位于同一条直线上,钢块与水平面间的动摩擦因数为μ,求碰后钢块能滑行的距离。(摆长的尺寸远大于摆球和钢块的尺寸)
解析:
设摆锤摆至少最低点时速度为v0,由机械能守恒定律得:
Mgl (1+sinα)=![]() ① (2分)
① (2分)
设摇锤与钢块碰撞后速度分别为v1、v2,则由动量守恒定律得:
Mv0=Mv1+mv2 ② (2分)
碰后摆锤上升到点过程机械能守恒,则有:
Mgl (1-sinα)=![]() ③ (2分)
③ (2分)
碰后对钢块在水平面上滑行至停下过程由动能定理得:
-μmgS=0-![]() ④ (2分)
④ (2分)
联立以①②③④式解得:
S=![]() ⑤ (2分)
⑤ (2分)

练习册系列答案
相关题目
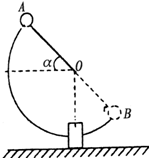 如图所示,摆锤的质量为M,摆杆长为l,其质量不计,摆杆初始位置OA与水平面成α角,释放后摆锤绕O轴无摩擦地做圆周运动,至最低点与质量为m的钢块发生碰撞,碰撞时间极短,碰后摆锤又上升至B点,A、B位于同一条直线上,钢块与水平面间的动摩擦因数为μ,求
如图所示,摆锤的质量为M,摆杆长为l,其质量不计,摆杆初始位置OA与水平面成α角,释放后摆锤绕O轴无摩擦地做圆周运动,至最低点与质量为m的钢块发生碰撞,碰撞时间极短,碰后摆锤又上升至B点,A、B位于同一条直线上,钢块与水平面间的动摩擦因数为μ,求