题目内容
【题目】如图所示,在平面直角坐标系中存在有界匀强电场区域,电场方向沿y轴负方向,电场强度大小为E.边界为y轴,右边界为平行于y轴的虚线,右边界与x轴交点横坐标等于L(L>0)。一带电粒子(不计重力)从坐标原点O处以初速度v0沿x轴正方向射入电场区域,粒子所带电荷量等于-q,质量为m。求:
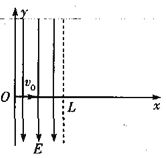
(1)带电粒子从电场右边界射出时的速度v的大小;
(2)若电场方向在平面内沿逆时针方向旋转θ(θ<90°)角,恰好使粒子不射出电场右边界,sinθ的值是多少。
【答案】(1) (2)
(2)![]()
【解析】解(1)设粒子在电场运动过程所用时间等于t,出射时速度的竖直分量为vy,加速度为a。粒子在电场中做匀变速曲线运动,根据匀变速曲线运动规律可得:
沿x轴方向:L= v0t
沿y轴方向:vy= at
对粒子,由牛顿第二定律qE=ma
粒子出电场的速度![]()
联立各式,解得
(2)将电场力沿水平和竖直两个方向分解,
则沿水平方向有-qEsinθ=-ma
竖直方向受力不影响水平方向分速度
则![]() =-2ax(2分)
=-2ax(2分)
联立解得sinθ=![]()

练习册系列答案
相关题目