题目内容
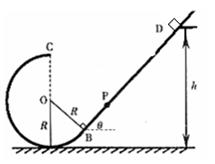
如图所示,一个小球从光滑斜面上无初速度滚下,然后进入一个半径为r=0.5m的光滑圆形轨道的内侧,小球恰能通过轨道的最高点,则小球下滑的高度h为 m,通过最低点时小球的向心加速度为 m/s2。(g="10" m/s2)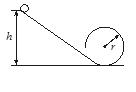
1.25 50
解析试题分析:在圆轨道最高处,小球恰好通过轨道的最高点,只有重力提供向心力,可以由牛顿第二定律 知道此处的速度为
知道此处的速度为 , 由机械能守恒
, 由机械能守恒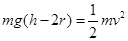 ,解出
,解出 m;设小球到最低点时的速度为
m;设小球到最低点时的速度为 ,由机械能守恒
,由机械能守恒
 m/s, 通过最低点时小球的向心加速度
m/s, 通过最低点时小球的向心加速度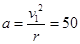 m/s2。
m/s2。
考点:牛顿第二定律 机械能守恒定律 向心加速度

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
如图所示,在小车内用细绳a和b系住一个小球,绳a处于斜向上的方向,拉力为Fa,绳b处于水平方向,拉力为Fb,小车和小球均保持静止.现让小车从静止开始向右做匀加速运动,此时小球相对于车厢的位置仍保持不变,则两根细绳的拉力变化情况是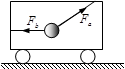
| A.Fa变大,Fb不变 | B.Fa变大, Fb变小 |
| C.Fa变大,Fb变大 | D.Fa不变, Fb变小 |

 m/s
m/s  m/s
m/s 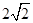 m/s
m/s 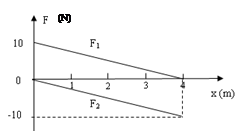

 ,上表面光滑,小车与地面间的摩擦力极小,可以忽略不计。可视为质点的物块B置于A的最右端,B的质量
,上表面光滑,小车与地面间的摩擦力极小,可以忽略不计。可视为质点的物块B置于A的最右端,B的质量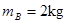 。现对A施加一个水平向右的恒力F=10N,A运动一段时间后,小车左端固定的挡板B发生碰撞,碰撞时间极短,碰后A、B粘合在一起,共同在F的作用下继续运动,碰撞后经时间t=0.6s,二者的速度达到
。现对A施加一个水平向右的恒力F=10N,A运动一段时间后,小车左端固定的挡板B发生碰撞,碰撞时间极短,碰后A、B粘合在一起,共同在F的作用下继续运动,碰撞后经时间t=0.6s,二者的速度达到 。求
。求