题目内容
光滑绝缘水平面上有一个带电质点正以速度v向右匀速运动.如果加一个水平方向的匀强电场,经过一段时间后,该质点的速度与初始速度等大反向;如果不加电场,而加一竖直向下的匀强磁场,经过相同的时间,该质点的速度也与初始速度等大反向,求匀强电场的电场强度E和匀强磁场的磁感应强度B的比值
.

| E |
| B |

带电质点(设电量为q,质量为m)所受重力与水平面的支持力平衡,只加电场时,根据牛顿第二定律,有:qE=ma
根据速度时间关系公式,有:-v=v-at
解得:E=
只加磁场时,根据牛顿第二定律,有:qvB=m
则周期:T=
=
质点经t时间速度等大反向,则:
t=(2n+1)?
(n=0,1,2,…)
解得:B=
(n=0,1,2,…)
所以
=
(n=0,1,2,…)
答:匀强电场的电场强度E和匀强磁场的磁感应强度B的比值
=
(n=0,1,2,…).
根据速度时间关系公式,有:-v=v-at
解得:E=
| 2mv |
| qt |
只加磁场时,根据牛顿第二定律,有:qvB=m
| v2 |
| r |
则周期:T=
| 2πr |
| v |
| 2πm |
| qB |
质点经t时间速度等大反向,则:
t=(2n+1)?
| T |
| 2 |
解得:B=
| (2n+1)πm |
| qt |
所以
| E |
| B |
| 2v |
| (2n+1)π |
答:匀强电场的电场强度E和匀强磁场的磁感应强度B的比值
| E |
| B |
| 2v |
| (2n+1)π |

练习册系列答案
相关题目
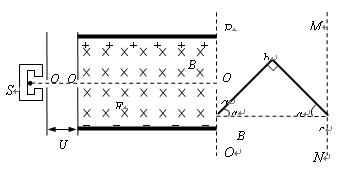
 的加速电场后,进入一圆形匀强磁场区,磁场方向垂直于圆面(以垂直圆面向里为正方向),磁场区的中心为O,半径为
的加速电场后,进入一圆形匀强磁场区,磁场方向垂直于圆面(以垂直圆面向里为正方向),磁场区的中心为O,半径为 ,荧光屏MN到磁场区中心O的距离为
,荧光屏MN到磁场区中心O的距离为 。当不加磁场时,电子束将通过O点垂直打到屏幕的中心
。当不加磁场时,电子束将通过O点垂直打到屏幕的中心 点,当磁场的磁感应强度随时间按图9乙所示的规律变化时,在荧光屏上得到一条长为
点,当磁场的磁感应强度随时间按图9乙所示的规律变化时,在荧光屏上得到一条长为 的亮线。由于电子通过磁场区的时间很短,可以认为在每个电子通过磁场区的过程中磁场的磁感应强度不变。已知电子的电荷量为
的亮线。由于电子通过磁场区的时间很短,可以认为在每个电子通过磁场区的过程中磁场的磁感应强度不变。已知电子的电荷量为 ,质量为
,质量为 ,不计电子之间的相互作用及所受的重力。求:
,不计电子之间的相互作用及所受的重力。求: (1)电子打到荧光屏上时速度的大小
(1)电子打到荧光屏上时速度的大小 。
。
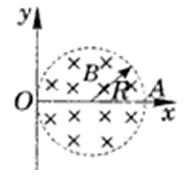
 垂直于纸面的直线为轴旋转磁场区域,能使穿过磁场区且偏转角最大的α粒子射到正方向的y轴上,则圆形磁场区的直径OA至少应转过多大角度?
垂直于纸面的直线为轴旋转磁场区域,能使穿过磁场区且偏转角最大的α粒子射到正方向的y轴上,则圆形磁场区的直径OA至少应转过多大角度?