Question

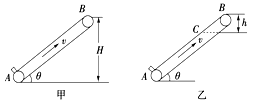
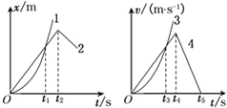
【题目】某实验小组做了如下实验，装置如图甲所示．竖直平面内的光滑轨道由倾角为θ的斜面轨道AB和圆弧轨道BCD组成，将质量m=0．1kg的小球，从轨道AB上高H处的某点静止滑下，用压力传感器测出小球经过圆弧最高点D时对轨道的压力F，改变H的大小，可测出相应的F大小，F随H的变化关系如图乙所示．g=10m/s2．求：

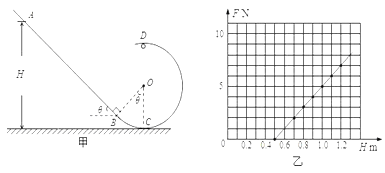
（1）圆轨道的半径R．

（2）若小球从D点水平飞出后又落到斜面上，其中最低的位置与圆心O等高，求θ的值．

Answer 1

【答案】（1）； （2）

【解析】

试题分析：（1）小球经过D点时，满足竖直方向的合力提供圆周运动向心力即：

从A到D的过程中只有重力做功，根据动能定理有：

联立解得：

由题中给出的F-H图象知斜率 即

所以可得

（2）小球离开D点做平抛运动，根据几何关系知，小球落地点越低平抛的射程越小，即题设中小球落地点位置最低对应小球离开D点时的速度最小．

根据临界条件知，小球能通过D点点时的最小速度为:

解得：

小球落地地点在斜面上与圆心等高，故可知小球平抛时下落的距离为R

所以小球平抛的射程:

由几何关系可知，