题目内容
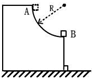一质量为m的小物块，由静止开始，沿半径为R的| 1 |
| 4 |
分析：物块从光滑的圆弧轨道下滑过程中，只有重力做功，机械能守恒，由机械能守恒定律求出物块滑到轨道末端时的速度大小．物块滑到轨道末端时，由重力和轨道的支持力的合力提供向心力，根据牛顿第二定律求出轨道的支持力，由牛顿第三定律得到物块对轨道的压力．
解答：解：设物块滑到轨道末端时的速度大小为v，根据机械能守恒定律得
mgR=
mv2
得到v=
物块经过轨道末端时，由牛顿第二定律得
N-mg=m
代入解得，轨道对物块的支持力大小为N=3mg，方向竖直向上则由牛顿第三定律得：物块对轨道的压力大小为N′=3mg，方向竖直向下．
故选D
mgR=
| 1 |
| 2 |
得到v=
| 2gR |
物块经过轨道末端时，由牛顿第二定律得
N-mg=m
| v2 |
| R |
代入解得，轨道对物块的支持力大小为N=3mg，方向竖直向上则由牛顿第三定律得：物块对轨道的压力大小为N′=3mg，方向竖直向下．
故选D
点评：本题是机械能守恒定律和牛顿运动定律结合处理圆周运动动力学问题，本题的结论N=3mg与轨道半径无关．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
如图，质量为M的楔形物A静置在水平地面上，其斜面的倾角为θ．斜面上有一质量为m的小物块B，B与斜面之间存在摩擦．用恒力F沿斜面向上拉B，使之匀速上滑．在B运动的过程中，楔形物块A始终保持静止．关于相互间作用力的说法正确的是（ ）
如图，AB为斜面轨道，与水平方向成45°角，BC为水平轨道，两轨道在B处通过一段小圆弧相连接，一质量为m的小物块，自轨道AB的A处从静止开始沿轨道下滑，最后停在轨道上的C点，已知A点高h，物块与轨道间的滑动摩擦系数为μ，求：
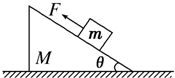如图所示，质量为M的楔形物块静止在水平地面上，其斜面的倾角为θ．斜面上有一质量为m的小物块，小物块与斜面之间存在摩擦．用恒力F沿斜面向上拉，使之匀速上滑．在小物块运动的过程中，楔形物块始终保持静止，则（ ）| A、地面对楔形物块的支持力为（M+m）g | B、地面对楔形物块的摩擦力为零 | C、楔形物块对小物块摩擦力可能为零 | D、小物块一定受到四个力作用 |
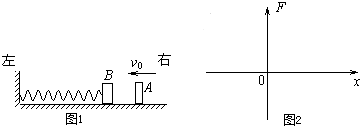
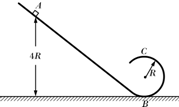如图所示，固定在竖直平面内的光滑轨道，由一段斜直轨道和与之相切的圆形轨道连接而成，圆形轨道半径为R．一质量为m的小物块（可视为质点）从斜直轨道上的A点由静止开始下滑，然后沿圆形轨道运动．A点距轨道最低点的竖直高度为4R．已知重力加速度为g．求：