题目内容
6.质量为m的小球在竖直平面内的圆形轨道的内侧运动,经过最高点而不脱离轨道的临界速度为v,当小球以3v的速度经过最高点时,对轨道的压力是( )| A. | 8mg | B. | 0 | C. | 5mg | D. | 9mg |
分析 对小球在最高点受力分析,找出向心力来源,根据牛顿第二、三定律和向心力公式列方程求解.
解答 解:当小球以速度v经内轨道最高点时不脱离轨道,小球仅受重力,重力充当向心力,有 mg=m$\frac{{v}^{2}}{r}$
当小球以速度3v经内轨道最高点时,小球受重力G和向下的支持力N,如图,合外力充当向心力,有 mg+N=m$\frac{{(3v)}^{2}}{r}$;
又由牛顿第三定律得到,小球对轨道的压力与轨道对小球的支持力相等,N′=N;
由以上三式得到,N′=8mg;
故选:A.
点评 本题关键对小球进行受力分析,找出向心力来源;同时,要注意题中要求的为轨道对小球的压力,而非支持力!

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,用两根等长丝线悬在同一点的带电小球受静电斥力而相互分开,两根悬线和竖直方向的夹角分别为α和β,A球质量为m1、B球质量为m2,则( )
如图,用两根等长丝线悬在同一点的带电小球受静电斥力而相互分开,两根悬线和竖直方向的夹角分别为α和β,A球质量为m1、B球质量为m2,则( )
 如图,用两根等长丝线悬在同一点的带电小球受静电斥力而相互分开,两根悬线和竖直方向的夹角分别为α和β,A球质量为m1、B球质量为m2,则( )
如图,用两根等长丝线悬在同一点的带电小球受静电斥力而相互分开,两根悬线和竖直方向的夹角分别为α和β,A球质量为m1、B球质量为m2,则( )| A. | 若α>β,则A球带的电量一定比B球多 | B. | 若α>β,则A球的质量一定比B球小 | ||
| C. | $\frac{sinα}{sinβ}$=$\frac{{m}_{2}}{{m}_{1}}$ | D. | $\frac{tanα}{tanβ}$=$\frac{{m}_{2}}{{m}_{1}}$ |
18.设某种物质的摩尔质量为μ,分子间平均距离为d,已知阿伏加德罗常数为NA,则该物质的密度ρ可表示为( )
| A. | ρ=$\frac{6μ}{π{d}^{3}{N}_{A}}$ | B. | ρ=$\frac{μ}{{d}^{3}{N}_{A}}$ | C. | ρ=$\frac{3μ}{4π{d}^{3}{N}_{A}}$ | D. | ρ=$\frac{8μ}{πd{N}_{A}}$ |
15.跳高运动员从地面上起跳的瞬间,下列说法中正确的是( )
| A. | 运动员给地面的压力小于运动员受到的重力 | |
| B. | 地面给运动员的支持力大于运动员受到的重力 | |
| C. | 地面给运动员的支持力大于运动员对地面的压力 | |
| D. | 地面给运动员的支持力的大小和运动员对地面的压力是一对作用力和反作用力 |
16. 如图所示,有一束单色光平行于等边三棱镜的截面ABC由空气射向E点,并折射到F点,已知入射方向与边AB的夹角为θ=30°,E,F分别为边AB,BC的中点,AC=a,光在真空中的传播速度为c.则下列说法正确的是( )
如图所示,有一束单色光平行于等边三棱镜的截面ABC由空气射向E点,并折射到F点,已知入射方向与边AB的夹角为θ=30°,E,F分别为边AB,BC的中点,AC=a,光在真空中的传播速度为c.则下列说法正确的是( )
 如图所示,有一束单色光平行于等边三棱镜的截面ABC由空气射向E点,并折射到F点,已知入射方向与边AB的夹角为θ=30°,E,F分别为边AB,BC的中点,AC=a,光在真空中的传播速度为c.则下列说法正确的是( )
如图所示,有一束单色光平行于等边三棱镜的截面ABC由空气射向E点,并折射到F点,已知入射方向与边AB的夹角为θ=30°,E,F分别为边AB,BC的中点,AC=a,光在真空中的传播速度为c.则下列说法正确的是( )| A. | 该三棱镜的折射率为$\sqrt{3}$ | B. | 发生全反射的临界角小于30° | ||
| C. | 在BC边无光出射 | D. | 光从E点到F点传播的时间为$\frac{a}{2c}$ |
 将单摆装置竖直悬挂于某一深度为h(未知)且开口向下的小筒中(单摆的下部分露于筒外),如图(甲)所示,将悬线拉离平衡位置一个小角度后由静止释放,设单摆振动过程中悬线不会碰到筒壁,如果本实验的长度测量工具只能测量出筒的下端口到摆球球心之距离L,并通过改变L而测出对应的摆动周期为T,再以T2为纵轴、L为横轴做出函数关系图象,那么就可以通过此图象得出小筒的深度h和当地的重力加速度
将单摆装置竖直悬挂于某一深度为h(未知)且开口向下的小筒中(单摆的下部分露于筒外),如图(甲)所示,将悬线拉离平衡位置一个小角度后由静止释放,设单摆振动过程中悬线不会碰到筒壁,如果本实验的长度测量工具只能测量出筒的下端口到摆球球心之距离L,并通过改变L而测出对应的摆动周期为T,再以T2为纵轴、L为横轴做出函数关系图象,那么就可以通过此图象得出小筒的深度h和当地的重力加速度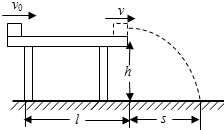 如图所示,质量为m的小物块在粗糙水平桌面上做直线运动,经距离l后以速度v飞离桌面,最终落在水平地面上.已知l=1.4m,v=3.0m/s,m=0.10kg,物块与桌面间的动摩擦因数μ=0.25,桌面高h=0.45m.不计空气阻力,重力加速度取10m/s2.求:(结果保留2位有效数字)
如图所示,质量为m的小物块在粗糙水平桌面上做直线运动,经距离l后以速度v飞离桌面,最终落在水平地面上.已知l=1.4m,v=3.0m/s,m=0.10kg,物块与桌面间的动摩擦因数μ=0.25,桌面高h=0.45m.不计空气阻力,重力加速度取10m/s2.求:(结果保留2位有效数字)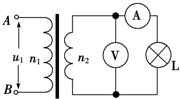 (A)如图,理想变压器原、副线圈匝数比n1:n2=2:1,V和A均为理想电表,灯泡电阻R1=6Ω,AB端电压u1=12$\sqrt{2}$•sin 100πt(V).求:
(A)如图,理想变压器原、副线圈匝数比n1:n2=2:1,V和A均为理想电表,灯泡电阻R1=6Ω,AB端电压u1=12$\sqrt{2}$•sin 100πt(V).求: 如图所示,在光滑的圆锥体顶端用长为L的细线悬挂一质量为m的小球.圆锥体固定在水平面上不动,其轴线沿竖直方向,母线与轴线之间的夹角为30°.小球以速度v绕圆锥体轴线在水平面内做匀速圆周运动,求
如图所示,在光滑的圆锥体顶端用长为L的细线悬挂一质量为m的小球.圆锥体固定在水平面上不动,其轴线沿竖直方向,母线与轴线之间的夹角为30°.小球以速度v绕圆锥体轴线在水平面内做匀速圆周运动,求