题目内容
16.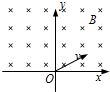 如图所示,在x轴的上方(y>0的空间内)存在着垂直于纸面向里、磁感应强度为B的匀强磁场,一对正、负电子从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成30°角,若电子的质量为m,电量为e:
如图所示,在x轴的上方(y>0的空间内)存在着垂直于纸面向里、磁感应强度为B的匀强磁场,一对正、负电子从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成30°角,若电子的质量为m,电量为e:(1)画出正、负电子运行轨迹图,求正、负电子在磁场中作圆周运动的轨道半径;
(2)正、负电子在磁场中运动的时间.
(3)正、负电子从磁场中射出时的位置.
分析 (1)电子在磁场中做匀速圆周运动,应用左手定则判断出电子所受洛伦兹力方向,然后作出电子的运动轨迹,应用牛顿第二定律求出电子的轨道半径.
(2)求出电子在磁场中做圆周运动转过的圆心角,然后根据电子做圆周运动的周期求出电子的运动时间.
(3)根据电子的轨道半径,应用几何知识求出电子射出磁场的位置.
解答 解:(1)电子在磁场中做匀速圆周运动,由左手定则可知,正电子沿逆时针方向转动,
负电子沿顺时针方向转动,电子运动轨迹如图所示:
电子做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:evB=m$\frac{{v}^{2}}{r}$,解得:r=$\frac{mv}{eB}$;
(2)电子在磁场中做圆周运动的周期:T=$\frac{2πm}{eB}$,
正电子在磁场中转过的圆心角:θ1=300°,θ2=60°,
正电子在磁场中的运动时间:t1=$\frac{{θ}_{1}}{360°}$T=$\frac{5πm}{3eB}$,
负电子在磁场中的运动时间:t2=$\frac{{θ}_{2}}{360°}$T=$\frac{πm}{3eB}$;
(3)电子离开磁场时与x轴的交点距离:d=2rcos60°=$\frac{mv}{eB}$,
正电子从磁场中射出的位置坐标为:(-$\frac{mv}{eB}$,0),
负电子从磁场中射出的位置坐标为:($\frac{mv}{eB}$,0);
答:(1)出正、负电子运行轨迹图如图所示,正、负电子在磁场中作圆周运动的轨道半径为$\frac{mv}{eB}$;
(2)正、负电子在磁场中运动的时间分别为:$\frac{5πm}{3eB}$、$\frac{πm}{3eB}$;
(3)正电子从磁场中射出的位置坐标为:(-$\frac{mv}{eB}$,0),
负电子从磁场中射出的位置坐标为:($\frac{mv}{eB}$,0).
点评 本题考查了电子在磁场中的运动,电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,分析清楚电子的运动过程,应用牛顿第二定律与电子做圆周运动的周期公式可以解题.

 如图所示,绝缘金属平行板电容器充电后,静电计的指针偏转一定角度,若不改变两极板带的电量而减小两极板间的距离,同时在两极板间插入电介质,则( )
如图所示,绝缘金属平行板电容器充电后,静电计的指针偏转一定角度,若不改变两极板带的电量而减小两极板间的距离,同时在两极板间插入电介质,则( )| A. | 电容器的电容将增小 | B. | 电容器的电容将增大 | ||
| C. | 静电计指针的偏转角度会减小 | D. | 静电计指针的偏转角度会增大 |
| A. | 物体的重心可以不在物体的几何中心上 | |
| B. | 劲度系数越大的弹簧,产生的弹力越大 | |
| C. | 静摩擦力的大小是在零和最大静摩擦力之间发生变化 | |
| D. | 动摩擦因数与物体之间的压力成反比,与滑动摩擦力成正比 |
 如图所示P和Q为两平行金属板,板间电压恒为U,在P板附近有一电子由静止开始向Q板运动,则关于电子在两板间运动情况,下列说法正确的是( )
如图所示P和Q为两平行金属板,板间电压恒为U,在P板附近有一电子由静止开始向Q板运动,则关于电子在两板间运动情况,下列说法正确的是( )| A. | 两板间距离越大,加速时间越长 | |
| B. | 两板间距离越小,加速度越大,则电子到达Q板时获得的速率就越大 | |
| C. | 电子到达Q板时获得的速率与两板间距离无关,仅与加速电压U有关 | |
| D. | 电子的加速度和末速度都与两板间距离无关 |
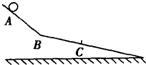 如图,两光滑斜面在B处连接,小球从A处由静止释放,经过B、C两点时速度大小分别为3m/s和4m/s,AB=BC.设球经过B点前后速度大小不变,则球在AB、BC段的加速度大小之比及球由A运动到C过程中的平均速率分别为( )
如图,两光滑斜面在B处连接,小球从A处由静止释放,经过B、C两点时速度大小分别为3m/s和4m/s,AB=BC.设球经过B点前后速度大小不变,则球在AB、BC段的加速度大小之比及球由A运动到C过程中的平均速率分别为( )| A. | 3:4,2.1 m/s | B. | 9:16,2.5m/s | C. | 9:7,2.1m/s | D. | 9:7,2.5 m/s |
| A. | 1.8m,镜子的顶边与头顶平齐 | |
| B. | 1.8m,镜子的顶边与双眼平齐 | |
| C. | 0.9m,镜子的顶边与双眼平齐 | |
| D. | 0.9m,镜子的顶边在头顶与双眼之间 |
 如图所示,A、B、C三点都在匀强电场中,已知AC⊥BC,∠ABC=60°,BC=40cm.把一个电荷量q=10-5C的正电荷从A移到B,电场力做功为零;从B移到C,克服电场力做功3.46×10-3J.试求该匀强电场的电场强度(包括大小和方向).并画出经 A、B、C三点电场线.
如图所示,A、B、C三点都在匀强电场中,已知AC⊥BC,∠ABC=60°,BC=40cm.把一个电荷量q=10-5C的正电荷从A移到B,电场力做功为零;从B移到C,克服电场力做功3.46×10-3J.试求该匀强电场的电场强度(包括大小和方向).并画出经 A、B、C三点电场线.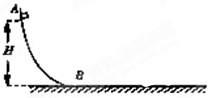 如图所示,质量为m的滑块在离地面高H=3.2m的光滑弧形轨道AB上由静止开始下滑,g取10m/s2,求:
如图所示,质量为m的滑块在离地面高H=3.2m的光滑弧形轨道AB上由静止开始下滑,g取10m/s2,求: