题目内容
某同学要进行探究小车速度随时间变化的规律实验，在试验中获得了一条纸带，并从中选取了7个计数点，如图1所示，其中两计数点间的时间间隔T=0.1s，测出OA=3.18cm，OB=7.54cm，OC=13.09cm，OD=19.83cm，OE=27.75cm，OF=36.87cm，则
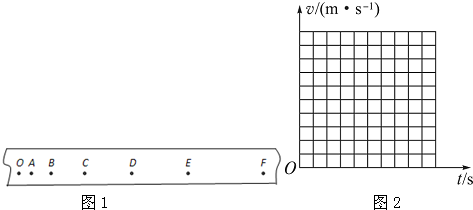
（1）该同学要计算打下C点时的速度，可用公式VC=
．（用字母表示）
（2）请用描点法在如图2所示中做出v-t图象（要求要有5个点）
（3）图象的纵轴截距表示的是
（4）若要计算小车的加速度，可用公式a=
（用字母表示）；算出结果为a=
（1）该同学要计算打下C点时的速度，可用公式VC=
| OD-OB |
| 2T |
| OD-OB |
| 2T |
（2）请用描点法在如图2所示中做出v-t图象（要求要有5个点）
（3）图象的纵轴截距表示的是
打下O点时的速度
打下O点时的速度
；（4）若要计算小车的加速度，可用公式a=
| OF-2OC |
| 9T2 |
| OF-2OC |
| 9T2 |
1.19
1.19
m/s2．（结果保留三位有效数字）分析：根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上个点的瞬时速度大小；根据描点法画出v-t图，根据作差法求出加速度．
解答：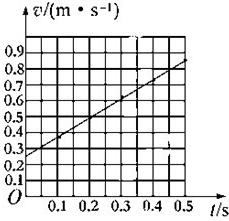
解：（1）C点的瞬时速度等于B到D的平均速度，得：
vC=
=
m/s=0.615m/s
同理，可以计算出ABD等点的速度：
vA=
=0.377m/s
vB=
=0.496m/s
vD=
=0.733m/s
vE=
=0.852m/s
v-t图象如图所示：
（3）图象的纵轴截距表示的是当时间为零时的速度，即为小车打下O点时的速度；
（4）根据作差法得：
a=
=
带入数据得：a=
=1.19m/s2
故答案为：（1）
；（2）如图所示；（3）打下O点时的速度；（4）
；1.19
解：（1）C点的瞬时速度等于B到D的平均速度，得：vC=
| OD-OB |
| 2T |
| 0.1983-0.0754 |
| 0.2 |
同理，可以计算出ABD等点的速度：
vA=
| OB |
| 2T |
vB=
| OC-OA |
| 2T |
vD=
| OE-OC |
| 2T |
vE=
| OF-OD |
| 2T |
v-t图象如图所示：
（3）图象的纵轴截距表示的是当时间为零时的速度，即为小车打下O点时的速度；
（4）根据作差法得：
a=
| xEF+xDE+xCD-xBC-xAB-xOA |
| 9T2 |
| OF-2OC |
| 9T2 |
带入数据得：a=
| 0.3687-0.1309×2 |
| 0.09 |
故答案为：（1）
| OD-OB |
| 2T |
| OF-2OC |
| 9T2 |
点评：要提高应用匀变速直线的规律以及推论解答实验问题的能力，在平时练习中要加强基础知识的理解与应用．
练习册系列答案
相关题目
（1）某同学要进行探究小车速度随时间变化的关系的实验，请在下面列出的实验器材中，选出本实验中不需要的器材填在横线上（填编号）：
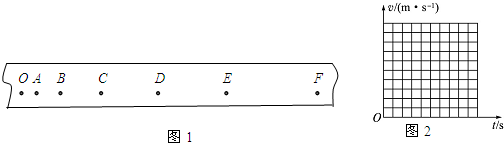
某同学要进行探究小车速度随时间变化的规律实验，在实验中获得了一条纸带，并从中选取7个计数点，如图所示，其中相邻两计数点时间间隔T=0.1s，测出OA距离s1=3.18cm，OB距离s2=7.54cm，OC距离s3=13.09cm，OD距离s4=19.83cm，OE距离s5=27.75cm，OF距离s6=36.87cm，则（结果保留三位有效数字）