题目内容
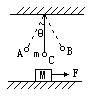
用长为l的细线把一个小球悬挂在倾角为θ的光滑斜面上,然后将小球偏离自然悬挂的位置拉到A点,偏角α≤5°,如图所示.当小球从A点无初速释放后,小球在斜面上往返振动的周期为多少?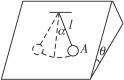

2π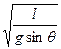
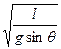
在光滑斜面上时,小球重力垂直于斜面的分力被斜面的支持力所平衡,另一个沿着斜面的分力G1=mgsinθ可分解成两个分力(如图所示):
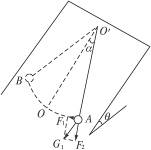
F1=G1sinα=mgsinθ·sinα
F1=G1cosα=mgsinθ·cosα
其中F2的方向始终沿着悬线,F1的方向垂直悬线.因此,F1就是使小球往返振动的回复力,即
F回=F1=mgsinθ·sinα.
在小振幅的条件下(α<5°),同样满足关系
sinα≈α=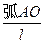 =
=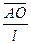 =
=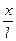
则:F回=mgsinθ·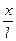
可见,放在光滑斜面上的单摆,同样做简谐运动,与竖直悬挂的单摆相比较,相当于重力加速度变为:g′=gsinθ.
所以振动周期:T=2π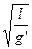 =2π
=2π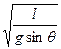 .
.

F1=G1sinα=mgsinθ·sinα
F1=G1cosα=mgsinθ·cosα
其中F2的方向始终沿着悬线,F1的方向垂直悬线.因此,F1就是使小球往返振动的回复力,即
F回=F1=mgsinθ·sinα.
在小振幅的条件下(α<5°),同样满足关系
sinα≈α=
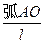 =
=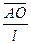 =
=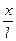
则:F回=mgsinθ·
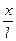
可见,放在光滑斜面上的单摆,同样做简谐运动,与竖直悬挂的单摆相比较,相当于重力加速度变为:g′=gsinθ.
所以振动周期:T=2π
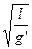 =2π
=2π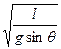 .
.
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目