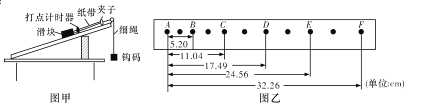
��Ŀ����
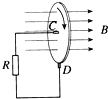
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ����һ����ֱ��ֽ�������Բ����ǿ�ų�����߽��ԭ��O��y���ϵĵ�a(0��L)��һ����Ϊm�������Ϊe�ĵ��Ӵ�a���Գ��ٶ�v0ƽ����x������������ų�������x���ϵ�b������ų�����ʱ�ٶȷ�����x��������ļн�Ϊ60������
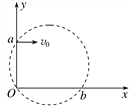
��1��������Բ���˶��İ뾶Ϊ���٣�
��2�������ڴų����˶���ʱ��Ϊ���٣�
��3�������ڴų�����Բ���˶���Բ������Ϊ���٣�
���𰸡���1��2L��2��![]() ��3����0����L��
��3����0����L��
��������������������ݵ��ӵ��ٶȷ���ȷ��Բ�ĵ�λ�ã�Ȼ�����ݼ��ι�ϵ���뾶��С���������ڹ�ʽ����ϵ���Բ���˶���Բ�Ľ��������ڴų����˶���ʱ�䡣���ݼ��ι�ϵ����������ڴų�����Բ���˶���Բ��������
��1��������ڴų��й켣�İ뾶Ϊr���˶��켣��ͼ���ɵõ����ڴų���ת����Բ�Ľ�Ϊ60��
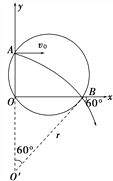
�ɼ��ι�ϵ�ɵã� ![]()
��ã��켣�뾶�� ![]()
��2�������ڴų���ת�������ڣ� ![]()
����ת����Բ�Ľ�Ϊ60����������ڴų����˶���ʱ��![]()
��3���ο���ͼ���ɼ��ι�ϵ��֪![]()
�����ڴų�����Բ���˶���Բ������Ϊ��0����L��

��ϰ��ϵ�д�
 ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
�����Ŀ