Question

【题目】两根材料相同的均匀直导线a和b串联在电路上，a长为，b长为。

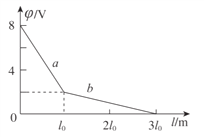
（1）若沿长度方向的电势随位置的变化规律如图所示，求：

①a、b两导线内电场强度大小之比；

②a、b两导线横截面积之比。

（2）以下对直导线内部做进一步分析：设导线单位体积内有n个自由电子，电子电荷量为e，自由电子定向移动的平均速率为v。现将导线中电流I与导线横截面积S的比值定义为电流密度，其大小用j表示。

①请建立微观模型，利用电流的定义推导：；

②从宏观角度看，导体两端有电压，导体中就形成电流；从微观角度看，若导体内没有电场，自由电子就不会定向移动。设导体的电阻率为ρ，导体内场强为E，试猜想j与E的关系并推导出j、ρ、E三者间满足的关系式。（解题过程中需要用到的物理量要在解题时作必要的说明）

Answer 1

【答案】（1）①②（2）①见解析②见解析

【解析】（1）①根据，由图像知：，代入可得，同理

根据，由已知

代入可得：

②因为两导线串联，所以电流，由欧姆定律，电阻定律

将，长度分别为和

代入可得：

（2）①在直导线内任选一个横截面S，在时间内以S为底，为高的柱体内的自由电子都将从此截面通过，由电流及电流密度的定义知：，其中

代入可得：

②（猜想：j与E成正比）设横截面积为S，长为l的导线两端电压为U，则

电流密度的定义为，将代入，得

导线的电阻

联立可得j、ρ、E三者间满足的关系式为：