题目内容
【题目】如图，半径R=1m的光滑半圆轨道AC与高8R的粗糙斜面轨道BD放在同一竖直平面内，BD部分水平长度为6R．两轨道之间由一条光滑水平轨道相连，水平轨道与斜轨道间有一段圆弧过渡．在水平轨道上，轻质弹簧被a、b两小球挤压（不连接），处于静止状态．同时释放两个小球，a球恰好能通过半圆轨道最高点A．已知a球质量为m1=2kg，b球质量为m2=1kg，小球b与斜面间动摩擦因素为μ= 
，重力力加速度为g=10m/s2 ． （sin37°=0.6，cos37°=0.8）求：
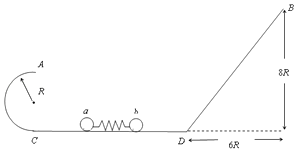
（1）a球经过C点时对轨道的作用力大小；
（2）释放小球前弹簧的弹性势能Ep；
（3）通过计算判断b球能否到达最高点B．
【答案】
（1）解：当a球恰好通过最高点时，根据 
得： 
= 
m/s= 
m/s，
根据动能定理得： 
，
代入数据解得： 
．
在C，根据牛顿第二定律得：： 
，
解得：Fc=6m1g=120N．
答：a球经过C点时对轨道的作用力大小为120N；
（2）解：a、b组成的系统动量守恒，规定a的速度方向为正方向，有：
0=m1vc﹣m2vD，
代入数据解得： 
m/s，
则弹簧的弹性势能为： 
= 
J=150J．
答：释放小球前弹簧的弹性势能为150J；
（3）解：b球从D点到达最高点过程中由动能定理： 
，
代入数据得l=10m．即b恰好能到达B点．
答：b恰好能到达B点．
【解析】（1）根据牛顿第二定律求出a球在A点的速度，结合动能定理求出C点的速度，根据牛顿第二定律求出a球经过C点时对轨道的作用力．（2）根据动量守恒定律求出b的速度，结合能量守恒求出弹簧的弹性势能．（3）根据动能定理求出b球上滑的位移大小，从而判断小球b能否到达最高点B．
【考点精析】关于本题考查的动量守恒定律和能量守恒定律，需要了解动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变；能量守恒定律：能量既不会消灭，也不会创生，它只会从一种形式转化为其他形式，或者从一个物体转移到另一个物体，而在转化和转移过程中，能量的总量保持不变才能得出正确答案．
