题目内容
7.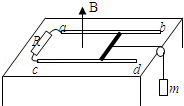 如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连,质量为m.电阻不计的导体棒垂直于导轨放置并可沿导轨自由滑动.整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B.导体棒的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一个质量也为m的物块相连,绳处于拉直状态.现若从静止开始释放物块(物块不会触地,且导体棒不脱离导轨),用h表示物块下落的高度,g表示重力加速度,其他电阻不计,则( )
如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连,质量为m.电阻不计的导体棒垂直于导轨放置并可沿导轨自由滑动.整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B.导体棒的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一个质量也为m的物块相连,绳处于拉直状态.现若从静止开始释放物块(物块不会触地,且导体棒不脱离导轨),用h表示物块下落的高度,g表示重力加速度,其他电阻不计,则( )| A. | 电阻R中的感应电流方向由a到c | |
| B. | 物体下落的最大加速度为g | |
| C. | 若h足够大,物体下落的最大速度为$\frac{mgR}{{B}^{2}{l}^{2}}$ | |
| D. | 通过电阻R的电量为$\frac{Blh}{R}$ |
分析 从静止开始释放物块,导体棒切割磁感线产生感应电流,根据右手定则判断感应电流方向.根据牛顿第二定律列式分析最大加速度.当导体棒匀速运动时,速度最大,由平衡条件和安培力的表达式结合推导出最大速度.根据感应电荷量表达式q=$\frac{△Φ}{R}$求解电量
解答 解:A、从静止开始释放物块,导体棒切割磁感线产生感应电流,由右手定则可知,电阻R中的感应电流方向由c到a,故A错误.
B、设导体棒所受的安培力大小为F,根据牛顿第二定律得:物块的加速度a=$\frac{mg-F}{2m}$,当F=0,即刚释放导体棒时,a最大,最大值为$\frac{1}{2}$g.故B错误.
C、物块和滑杆先做加速运动,后做匀速运动,此时速度最大,则有mg=F,而F=BIl,I=$\frac{Blv}{R}$,解得物体下落的最大速度为v=$\frac{mgR}{{B}^{2}{l}^{2}}$.故C正确.
D、通过电阻R的电量:q=$\frac{△Φ}{R}$=$\frac{B△S}{R}$=$\frac{Blh}{R}$.故D正确.
故选:CD.
点评 本题分析物体的运动情况是解题的基础,关键掌握要会推导安培力,知道感应电荷量表达式q=$\frac{△Φ}{R}$,式中R是回路的总电阻

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
18.将某物体分两个阶段举高到高处,每个阶段举高相同的高度,那么( )
| A. | 选不同的参考平面,在每个阶段物体重力势能的增量可能不相同 | |
| B. | 不论选什么参考平面,物体在末状态的重力势能都相等 | |
| C. | 选不同的参考平面,在各阶段重力做功不相等 | |
| D. | 选不同的参考平面,在各阶段重力做功相等 |
15.汽车在平直公路上以80kW的恒定功率从静止开始行驶,已知汽车的质量为2×103kg,运动过程中阻力f=4×103N,始终不变,则( )
| A. | 汽车运动过程中的牵引力不变 | |
| B. | 汽车所能达到的最大速度为40m/s | |
| C. | 汽车速度为10m/s时,加速度是2m/s2 | |
| D. | 汽车运动过程中加速度不断增大,速度也不断增大,直到最后做匀速运动 |
12. 质量为2kg的物体静止在足够大的水平面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力和滑动摩擦力大小视为相等.从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间t的变化规律如图所示.取重力加速度g=10m/s2,则物体在t=0到t=6s这段时间内的位移大小为( )
质量为2kg的物体静止在足够大的水平面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力和滑动摩擦力大小视为相等.从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间t的变化规律如图所示.取重力加速度g=10m/s2,则物体在t=0到t=6s这段时间内的位移大小为( )
 质量为2kg的物体静止在足够大的水平面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力和滑动摩擦力大小视为相等.从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间t的变化规律如图所示.取重力加速度g=10m/s2,则物体在t=0到t=6s这段时间内的位移大小为( )
质量为2kg的物体静止在足够大的水平面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力和滑动摩擦力大小视为相等.从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间t的变化规律如图所示.取重力加速度g=10m/s2,则物体在t=0到t=6s这段时间内的位移大小为( )| A. | 4 m | B. | 8 m | C. | 10m | D. | 12m |
19. 质量为m的子弹水平击中质量为M的木块而留在其中,甲、乙两同学分别画出了如图所示的示意图,若子弹射入木块的时间极短,则( )
质量为m的子弹水平击中质量为M的木块而留在其中,甲、乙两同学分别画出了如图所示的示意图,若子弹射入木块的时间极短,则( )
 质量为m的子弹水平击中质量为M的木块而留在其中,甲、乙两同学分别画出了如图所示的示意图,若子弹射入木块的时间极短,则( )
质量为m的子弹水平击中质量为M的木块而留在其中,甲、乙两同学分别画出了如图所示的示意图,若子弹射入木块的时间极短,则( )| A. | 当水平面光滑时甲图正确,当水平面粗糙时乙图正确 | |
| B. | 当子弹速度较大时甲图正确,当子弹速度较小时乙图正确 | |
| C. | 若水平面光滑,当M<m时,甲图正确,当M>m时乙图正确 | |
| D. | 不论水平面是否光滑,速度、质量大小关系如何,均是乙图正确 |
16. 如图6所示,单匝矩形线圈绕垂直于磁场的轴匀速转动,产生交流电的电动势瞬时值表达式是e=500sin50π•tV,下列说法中正确的是( )
如图6所示,单匝矩形线圈绕垂直于磁场的轴匀速转动,产生交流电的电动势瞬时值表达式是e=500sin50π•tV,下列说法中正确的是( )
 如图6所示,单匝矩形线圈绕垂直于磁场的轴匀速转动,产生交流电的电动势瞬时值表达式是e=500sin50π•tV,下列说法中正确的是( )
如图6所示,单匝矩形线圈绕垂直于磁场的轴匀速转动,产生交流电的电动势瞬时值表达式是e=500sin50π•tV,下列说法中正确的是( )| A. | t=0时刻线圈处于图示位置 | |
| B. | 从t=0时刻到第一次出现电动势最大值的时间是0.01s | |
| C. | 穿过线圈磁通量的最大值为$\frac{10}{π}$Wb | |
| D. | 电动势有效值为500$\sqrt{2}$V |
 宇航员在半径为R的星球表面完成了下列实验:他将一圆锥体固定,使其轴线竖直,再用长细线一端固定于圆锥体的顶点O,另一端拴一小球,让其在水平面内做匀速圆周运动,如图所示.他测得小球的运动周期为T时,恰好对圆锥体无压力,又测出O点到圆轨道面间的距离为h,已知万有引力常量为G.求:
宇航员在半径为R的星球表面完成了下列实验:他将一圆锥体固定,使其轴线竖直,再用长细线一端固定于圆锥体的顶点O,另一端拴一小球,让其在水平面内做匀速圆周运动,如图所示.他测得小球的运动周期为T时,恰好对圆锥体无压力,又测出O点到圆轨道面间的距离为h,已知万有引力常量为G.求: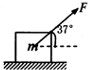 如图所示,一质量为m=2kg的物体在与水平方向成37°的拉力作用下处于静止状态,已知F=10N,sin37°=0.6,cos37°=0.8,g取10m/s2.
如图所示,一质量为m=2kg的物体在与水平方向成37°的拉力作用下处于静止状态,已知F=10N,sin37°=0.6,cos37°=0.8,g取10m/s2. 如图,在高H处有个小球A,以速度V1水平抛出,同时,地面上有个小球B以速度V2竖直上抛,两球在空中相遇,则从它们抛出到相遇所需的时间是$\frac{h}{{v}_{2}}$;两球抛出时的水平距离为$\frac{{v}_{1}h}{{v}_{2}}$.
如图,在高H处有个小球A,以速度V1水平抛出,同时,地面上有个小球B以速度V2竖直上抛,两球在空中相遇,则从它们抛出到相遇所需的时间是$\frac{h}{{v}_{2}}$;两球抛出时的水平距离为$\frac{{v}_{1}h}{{v}_{2}}$.