Question

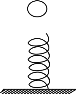
【题目】如图所示，一根均匀圆形直轻杆AC由粗细不同两段AB＝10m和BC＝2m组成，其中，AB段粗糙、BC段光滑，直轻杆AC垂直地固定在一块倾角为37°的楔形弹性斜面体上，弹性斜面体放在粗糙的水平面上，现有一质量为m＝2kg、孔径略大于直杆直径的圆环P，在沿杆向上的恒力F的作用下，从直轻杆AC的底端由静止开始沿杆向上运动，圆环P与杆间的动摩擦因数为0.1，当圆环P刚运动到B点时恒力F突然撤去，圆环刚好能到达顶端C，然后，再沿直轻杆下滑，环在整个运动过程中，弹性斜面体始终静止不动。重力加速度为g＝10m/s2，sin37°＝0.6，cos37°＝0.8．求：

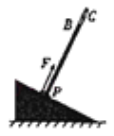
（1）在圆环P沿杆AB向上运动的过程中，地面对弹性斜面体的摩擦力；

（2）恒力F的最大功率；

（3）环从开始运动到第二次碰撞弹性斜面体的过程中，系统产生的热量。

Answer 1

【答案】（1）10.32N，方向水平向左 （2）115.4W （3）48J

【解析】

(1)环与直轻杆之间的滑动摩擦力大小为 fAB＝μmgcos53°

环对杆的压力 NAB＝mgcos53°

以弹性斜面体为研究对象，在水平方向上有

f0＝fABcos53°+NABcos37°

由以上两式解得地面对弹性斜面体的摩擦力 f0＝10.32N，方向水平向左。

(2)在圆环从A→C的过程中，由动能定理得:

Fx1-mg(x1+x2)sin53°-μmgx1cos53°＝0

在圆环从B→C的过程中，由机械能守恒得:

＝mgx2sin53°

恒力F的最大功率 Pm＝FvB

联立解得:Pm＝81.6W≈115.4W

(3)设第一次碰撞前圆环的动能为Ek，由动能定理得:

Fx1﹣2μmgx1cos53°＝Ek

设第一碰撞后向上运动的距离为x，由动能定理得

mgxsin53°﹣μmgxcos53°＝0﹣Ek

解得:x＝10.47m＞x1＝10m

系统产生的热量

Q＝(μmgcos53°)×x1×4

解得:Q＝48J.