题目内容
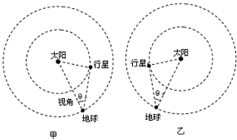 (2009?东莞模拟)地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为r=1.50×1011m,运转周期为T=3.16×107s.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角),如图甲或图乙所示.当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.已知某行星的最大视角为14.5°.求该行星的轨道半径和运转周期.(sin14.5°=0.25,最终计算结果保留两位有效数字)
(2009?东莞模拟)地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为r=1.50×1011m,运转周期为T=3.16×107s.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角),如图甲或图乙所示.当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.已知某行星的最大视角为14.5°.求该行星的轨道半径和运转周期.(sin14.5°=0.25,最终计算结果保留两位有效数字)分析:根据题意知道当行星处于最大视角处时,地球和行星的连线应与行星轨道相切,运用几何关系求解问题.
地球与某行星围绕太阳做匀速圆周运动,根据万有引力提供向心力列出等式,表示出周期,然后去进行求解.
地球与某行星围绕太阳做匀速圆周运动,根据万有引力提供向心力列出等式,表示出周期,然后去进行求解.
解答:解:设行星的轨道半径为r′,运行周期为T′
当行星处于最大视角处时,地球和行星的连线应与行星轨道相切.
由几何关系可知:
r′=rsin14.5°=3.8×108m
地球与某行星围绕太阳做匀速圆周运动,根据万有引力提供向心力列出等式:
G
=mr
,
可得:
=
,
即:
=
,
可得:T′=
=4.0×106s
答:该行星的轨道半径是3.8×108m,运转周期是4.0×106s.
当行星处于最大视角处时,地球和行星的连线应与行星轨道相切.
由几何关系可知:
r′=rsin14.5°=3.8×108m
地球与某行星围绕太阳做匀速圆周运动,根据万有引力提供向心力列出等式:
G
| Mm |
| r2 |
| 4π2 |
| T2 |
可得:
| r3 |
| T2 |
| GM |
| 4π2 |
即:
| r3 |
| T2 |
| r′3 |
| T′2 |
可得:T′=
|
答:该行星的轨道半径是3.8×108m,运转周期是4.0×106s.
点评:向心力的公式选取要根据题目提供的已知物理量或要求解的物理量选取应用.
物理问题经常要结合数学几何关系解决.
物理问题经常要结合数学几何关系解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2009?东莞模拟)如图为氢原子的部分能级图.下列的叙述中正确的是( )
(2009?东莞模拟)如图为氢原子的部分能级图.下列的叙述中正确的是( )