题目内容
【题目】如图1所示是某质谱仪的模型简化图，P点为质子源，初速度不计的质子经电压加速后从O点垂直磁场边界射入，在边界OS的上方有足够大的垂直纸面的匀强磁场区域，B＝0.2T。a、b间放有一个宽度为Lab＝0.1cm的粒子接收器S，oa长度为2m。质子的比荷
，质子经电场、磁场后正好打在接收器上。
（1）磁场的方向是垂直纸面向里还是向外？
（2）质子进入磁场的角度范围如图2所示，向左向右最大偏角
，所有的质子要打在接收板上，求加速电压的范围（结果保留三位有效数字，取cos80＝0.99, 
）。
（3）将质子源P换成气态的碳I2与碳14原子单体，气体在P点电离后均帯一个单位正电（初速度不计），碳12的比荷
C／kg，碳14的比荷
保持磁感应强度不变，从O点入射的角度范围不变，加速电压可以在足够大的范围内改变。要使在任一电压下接收器上最多只能接收到一种粒子，求oa的最小值（结果保留三位有效数字，取
)
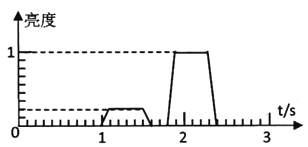
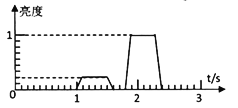
（4）第（3）问中的电离体经电压加速后，单位时间内从O点进入的粒子数保持不变，其中碳12占80％、碳14占20％。通过控制加速电压，使碳14在磁场中做圆周运动的半径与时间的关系R14＝0.9＋0.1t(cm）。请在图3中描绘出接收器上的亮度随时间的变化的图像（每毫秒内接收到的粒子越多越亮，1表示在这一过程中最亮时的亮度）。
【答案】（1）垂直纸面向外（2）
（3）
（4）如图所示：
【解析】
（1）由左手定则判断磁场的方向；
（2）粒子在电场中加速，在磁场中做匀速圆周运动，结合几何关系求解半径的范围，从而求解加速电压的范围；
（3）根据半径和荷质比的关系找到碳14和碳12做圆圆周运动的半径之比；结合几何关系找到oa的最小值；
（4）根据碳14在磁场中做圆周运动的半径与时间的关系结合第（3）问的计算画出图像。
（1）由左手定则可知，磁场的方向垂直纸面向外；
（2）粒子在电场中：
在磁场中：
，
其中的
解得204V≤U≤221V
（3）根据
可得
当2R12=Loa时
解得Loa>1.45m
（4）接收器上的亮度随时间的变化的图像如图；
