题目内容
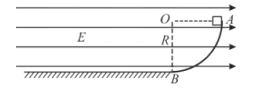
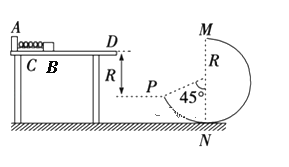
【题目】如图所示,水平桌面上有一轻弹簧,左端固定在A点,弹簧处于自然状态时其右端位于B点。水平桌面右侧有一竖直放置的内表面光滑、粗细可忽略不汁的圆管轨道MNP,其形状为半径R=0.8m的圆剪去了左上角![]() 的圆弧,MN为其竖直直径,P点到桌面的竖直距离也是R。用质量ml=0.2kg的物块将弹簧缓慢压缩到C点释放,物块过B点(B点为弹簧原长位置)时的速度为v0=6m/s,物块与桌面间的动摩擦因数μ=0.4,物块从桌面右边缘D点飞离桌面后,恰在P点无碰撞地进入圆管轨道。运动过程中,物块可视为质点,g=10m/s2
的圆弧,MN为其竖直直径,P点到桌面的竖直距离也是R。用质量ml=0.2kg的物块将弹簧缓慢压缩到C点释放,物块过B点(B点为弹簧原长位置)时的速度为v0=6m/s,物块与桌面间的动摩擦因数μ=0.4,物块从桌面右边缘D点飞离桌面后,恰在P点无碰撞地进入圆管轨道。运动过程中,物块可视为质点,g=10m/s2
(1)求m1运动至D点时的速度大小;
(2)求BP间的水平距离;
(3)计算分析m1经圆管轨道能否到达最高点M,若能则求到达最高点M时m1对轨道壁的压力.
【答案】(1)4 m/s(2)4.1 m(3)0.828N,方向竖直向下
【解析】
(1)设物块由D点以初速度vD做平抛运动,落到P点时其竖直速度为
![]()
![]()
得
vD=4 m/s
(2)m1做平抛运动用时为t,水平位移为s,
![]() ,s=vDt
,s=vDt
得
s=2R=1.6m
由已知条件可知,在桌面上过B点后初速v0=6 m/s,加速度
a=μg=4m/s2
减速到vD,BD间位移为
![]()
即BP水平间距为
s+s1=4.1m
(3)若物块能沿轨道到达M点,其速度为vM
![]()
由动能定理得
-mlg(R+Rcos![]() )=
)=![]()
解得
![]()
可见能到达M点,设轨道对物块的压力方向向下,大小为F,则
![]()
解得
F=(2-2![]() )N=-0.828N
)N=-0.828N
可见方向向上,根据牛顿第三定律:m1对轨道内壁的压力
![]() =F=0.828N
=F=0.828N
方向竖直向下.

【题目】某同学在“探究小车速度随时间变化的规律”实验中,选出了下面图所示的一条纸带(每两点间还有4个点没有画出来),纸带上方的数字为相邻两个计数点间的距离。打点计时器的电源频率为50 Hz。

(1)根据纸带上的数据,A、C、D、E点对应小车的瞬时速度已经填在表中,请你把B点对应的小车速度填在表格里。
位置 | A | B | C | D | E |
v /(m·s-1) | 0.655 | ____ | 1.296 | 1.600 | 1.865 |
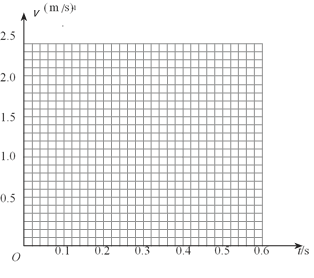
(2)在下面坐标系中,画出小车的v-t图像,(________)
并根据v-t图像判断小车是否做匀变速直线运动?________(填“是”或“否”)如果是,求出该匀变速直线运动的加速度___________。