题目内容
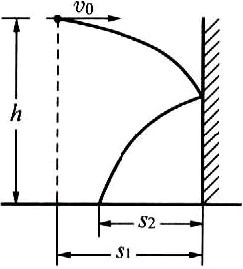
如图所示，在离地高为h、离竖直光滑墙的水平距离为s1处有一小球以v的速度向墙水平抛出，与墙碰后落地，不考虑碰撞的时间及能量损失，则落地点到墙的距离s2为多大？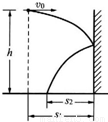
【答案】分析：小球抛出后做平抛运动，碰撞后小球水平速度不变，仍做平抛运动，根据平抛运动的特点即可求解．
解答：解：碰撞前，小球做平抛运动，碰撞后小球水平速度不变，仍做平抛运动，
所以则落地点到墙的距离s2等于没有墙壁时做平抛运动的水平位移减去s1，
所以h=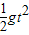
，解得：t=
水平方向有：x=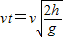
则落地点到墙的距离s2=x-s1=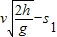
答：落地点到墙的距离s2为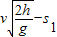
点评：本题主要考查了平抛运动的基本公式的直接应用，难度不大，属于基础题．
解答：解：碰撞前，小球做平抛运动，碰撞后小球水平速度不变，仍做平抛运动，
所以则落地点到墙的距离s2等于没有墙壁时做平抛运动的水平位移减去s1，
所以h=
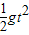，解得：t=水平方向有：x=
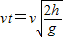
则落地点到墙的距离s2=x-s1=
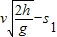
答：落地点到墙的距离s2为
点评：本题主要考查了平抛运动的基本公式的直接应用，难度不大，属于基础题．
练习册系列答案
相关题目
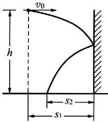如图所示，在离地高为h、离竖直光滑墙的水平距离为s1处有一小球以v0的速度向墙水平抛出，与墙碰后落地，不考虑碰撞的时间及能量损失，则落地点到墙的距离s2为多大？
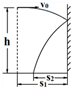如图所示，在离地高为h、离竖直光滑墙的水平距离为s1处有一小球以vo的速度向墙水平抛出，与墙碰后落地，不考虑碰撞的时间及能量损失，求：
