题目内容
4. 如图所示,质量m=2kg的小球用长L=5m的轻质细绳悬挂在距水平地面高H=10m的O点.现将细绳拉直至水平状态自A点无初速度释放小球,运动至悬点O的正下方B点时细绳恰好断裂,接着小球作平抛运动,落至水平地面上C点.不计空气阻力,重力加速度g取10m/s2.求:
如图所示,质量m=2kg的小球用长L=5m的轻质细绳悬挂在距水平地面高H=10m的O点.现将细绳拉直至水平状态自A点无初速度释放小球,运动至悬点O的正下方B点时细绳恰好断裂,接着小球作平抛运动,落至水平地面上C点.不计空气阻力,重力加速度g取10m/s2.求:(1)小球运动到B点时速度大小;(可以用机械能守恒定律进行求解)
(2)B点到C点的水平距离.
分析 (1)小球从A→B的过程中,绳子的拉力不做功,机械能守恒,可根据机械能守恒定律求出小球刚到达B点时的速度.
(2)细绳断裂后,小球做平抛运动,根据平抛运动的规律即可求解时间;再由水平方向的匀速运动规律求解水平位移.
解答 解:(1)小球从A→B过程,根据机械能守恒定律得:$mgL=\frac{1}{2}mv_B^2-0$
解得:vB=$\sqrt{2gL}$=10m/s
(2)小球从B→C过程做平抛运动,则有:$H-L=\frac{1}{2}g{t^2}$
解得:t=$\sqrt{\frac{2(H-L)}{g}}$=$\sqrt{\frac{2(10-5)}{10}}$s=1s
BC间的距离x=vt=10×1=10m;
答:(1)小球运动到B点时速度大小为10m/s;
(2)B点到C点的水平距离为10m
点评 本题考查机械能守恒定律及平抛运动规律,只要正确分析物理过程,明确机械能守恒及平抛运动规律的应用即可求解.

练习册系列答案
相关题目
15.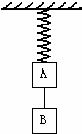 一根轻弹簧,下端系有质量为m的物体A,在A的下面再挂一个质量也是m的物体B,如图所示,在A、B保持静止时剪断AB间的细绳,如果A回到单独悬挂时的平衡位置的速率为v,而此时B的速率为u,那么在这段时间内弹力对A的冲量为( )
一根轻弹簧,下端系有质量为m的物体A,在A的下面再挂一个质量也是m的物体B,如图所示,在A、B保持静止时剪断AB间的细绳,如果A回到单独悬挂时的平衡位置的速率为v,而此时B的速率为u,那么在这段时间内弹力对A的冲量为( )
 一根轻弹簧,下端系有质量为m的物体A,在A的下面再挂一个质量也是m的物体B,如图所示,在A、B保持静止时剪断AB间的细绳,如果A回到单独悬挂时的平衡位置的速率为v,而此时B的速率为u,那么在这段时间内弹力对A的冲量为( )
一根轻弹簧,下端系有质量为m的物体A,在A的下面再挂一个质量也是m的物体B,如图所示,在A、B保持静止时剪断AB间的细绳,如果A回到单独悬挂时的平衡位置的速率为v,而此时B的速率为u,那么在这段时间内弹力对A的冲量为( )| A. | m(v+u) | B. | m(v-u) | C. | mv | D. | mu |
12.做抛体运动的物体,某一瞬间水平方向的速度是4m/s,竖直方向的速度是3m/s,则这个时候物体的实际速度是( )
| A. | 5m/s | B. | 1m/s | C. | 7m/s | D. | 0 |
19.汽车以恒定的速率通过一圆弧形拱桥,当它位于拱桥顶部时,下列说法中正确的是( )


| A. | 汽车处于超重状态 | |
| B. | 汽车对拱桥的压力等于其重力 | |
| C. | 汽车竖直方向上受重力、支持力和向心力的作用 | |
| D. | 汽车受到的重力和支持力的合力提供它所需的向心力,方向指向圆弧的圆心 |
9.一辆质量为m、额定功率为P的小车从静止开始以恒定的加速度a启动,所受阻力为Ff,经时间t,行驶距离x后达到最大速度vm,然后匀速运动,则从静止开始到达到最大速度过程中,机车牵引力所做的功为( )
| A. | Pt | B. | (Ff+ma)x | C. | $\frac{1}{2}$mvm2 | D. | $\frac{1}{2}$mvm2+Ffx |
 某实验小组在利用单摆测定当地重力加速度的实验中:
某实验小组在利用单摆测定当地重力加速度的实验中: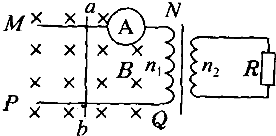 如图所示,MN、PQ是两条在水平面内、平行放置的光滑金属导轨,导轨的右端接理想变压器的原线圈,变压器的副线圈与阻值为R=0.5Ω的电阻组成闭合回路,变压器的原副线圈匝数之比n1:n2=2:1,导轨宽度为L=0.5m.质量为m=1kg的导体棒ab垂直MN、PQ放在导轨上,在水平外力作用下,从t=0时刻开始做往复运动,其速度随时问变化的规律是v=2sin$\frac{π}{2}$t(m/s),已知垂直轨道平面向下的匀强磁场的磁感应强度大小为B=1T,导轨、导体棒、导线和线圈的电阻均不计,电流表为理想交流电流表,导体棒始终在磁场中运动.求:
如图所示,MN、PQ是两条在水平面内、平行放置的光滑金属导轨,导轨的右端接理想变压器的原线圈,变压器的副线圈与阻值为R=0.5Ω的电阻组成闭合回路,变压器的原副线圈匝数之比n1:n2=2:1,导轨宽度为L=0.5m.质量为m=1kg的导体棒ab垂直MN、PQ放在导轨上,在水平外力作用下,从t=0时刻开始做往复运动,其速度随时问变化的规律是v=2sin$\frac{π}{2}$t(m/s),已知垂直轨道平面向下的匀强磁场的磁感应强度大小为B=1T,导轨、导体棒、导线和线圈的电阻均不计,电流表为理想交流电流表,导体棒始终在磁场中运动.求: