题目内容
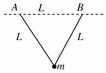
如右图所示两段长均为L的轻质线共同系住一个质量为m的小球，另一端分别固定在等高的A、B两点，A、B两点间距也为L，今使小球在竖直平面内做圆周运动，当小球到达最高点时速率为v，两段线中张力恰好均为零，若小球到达最高点时速率为2v，则此时每段线中张力大小为( )
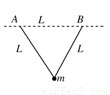
A.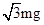 
B．
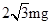
C．3mg D．4mg
【答案】
A
【解析】
试题分析：当小球到达最高点速率为v时，有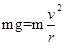
当小球到达最高点速率为2v时，应有
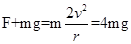，所以
，此时最高点各力如图所示，所以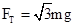
，A正确．
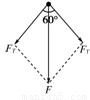
考点：牛顿第二定律；向心力．
点评：本题是竖直平面内圆周运动问题，关键是分析物体受力，确定向心力的来源．基本题，比较容易．
练习册系列答案
相关题目
如图所示，水平传送带水平段长l=3m，两皮带轮半径均为r=5cm，距地面高度h=3.2m，此时传送带静止．与传送带等高的光滑平台上，有一个可看成质点的小物体以v0的初速度滑上传送带，从传送带的右端飞出做平抛运动，水平射程是1.6m．已知物块与传送带间的动摩擦因数为0.2，求：
（2013?太原一模）如图所示，水平面AB与斜面BC相交于B点，其中BC段长x1=5m，AB段长x2=11m．一质量为m1的滑块P从C点由静止开始下滑，同时，另一质量为m2的滑块Q从A点以初速度v0=6m/s沿水平面开始向右运动，经过t=2.5s两滑块在运动中相遇．不考虑滑块经过B点时的机械能损失，已知θ=30°，两滑块与BC段的动摩擦因数均为μ1=
如图所示，传送带以v为7
mg B．2