题目内容
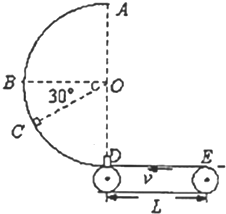 如图所示,传送带以v为7
如图所示,传送带以v为7| 2 |
(1)小滑块P从C处无初速度滑下,到轨道底端D碰撞刚结束的瞬间速度
(2)小滑块Q第一次碰撞后向右运动的最大距离以及此过程产生的热量
(3)移走小滑块Q,将小滑块P无初速度放在传送带E端,要使小滑块能通过A点,传送带DE段至少为多长?
分析:(1)根据机械能守恒定律求出小滑块P到达底端D时的速度.对于P、Q碰撞过程,根据动量守恒和机械能守恒列式,求解碰撞刚结束的瞬间P和Q的速度.
(2)小滑块Q滑上传送带先向右做匀减速运动到0,然后向左做匀加速直线运动,可知当速度减小为0时,向右运动的距离最大.根据动能定理求出向右运动的最大距离.由运动学公式求出运动的时间,求出这段时间内传送带的位移,从而得出滑块相对于传送带的位移,根据Q=fx相求出此过程中的热量.
(3)要使小滑块能通过E点,临界情况是通过N点时,轨道对滑块的弹力为0,有mg=m
,求出E点的临界速度,然后根据机械能守恒定律求出D点的速度,根据动能定理求出传送带的最小长度.
(2)小滑块Q滑上传送带先向右做匀减速运动到0,然后向左做匀加速直线运动,可知当速度减小为0时,向右运动的距离最大.根据动能定理求出向右运动的最大距离.由运动学公式求出运动的时间,求出这段时间内传送带的位移,从而得出滑块相对于传送带的位移,根据Q=fx相求出此过程中的热量.
(3)要使小滑块能通过E点,临界情况是通过N点时,轨道对滑块的弹力为0,有mg=m
| v2 |
| R |
解答:解:(1)小滑块P从C处到轨道底端D,根据能量守恒定律:m1gR(1-cos60°)=
m1
解得:v0=
=3
m/s
P、Q在D处发生弹性碰撞,由动量守恒和能量守恒得:
m1v0=m1v1+m2v2
m1v02=
m1v12+
m2v22
解得:v1=-
m/s,v2=2
m/s
即碰撞刚结束P的瞬时速度为
m/s,方向向左.
(2)小滑块Q做匀减速运动至停止时距离最大,由动能定理得:
-μm2gx=-
m2v22,
向右运动的距离最大为x=0.8m,运动时间为t=
=
=0.4
s
则:x相=vt+
v2t=6.4m,产生的热量为Q=μm2gx相=12.8J
(3)小滑块P恰能通过A点,由向心力公式得:m1g=m1
小滑块P从D到A,由动能定理得:-2m1gR=
m1vA2-
m1vD2
则:vD=
=3
m/s<7
m/s
则P一直在传送带DE段加速,且末速度恰为3
m/s,传送带最短,
由动能定理得:μm1gx′=
m1vD2
传送带至少为:x′=
=9m
答:
(1)小滑块P从C处无初速度滑下,到轨道底端D碰撞刚结束的瞬间速度为
m/s.
(2)小滑块Q第一次碰撞后向右运动的最大距离为6.4m,此过程产生的热量为12.8J.
(3)移走小滑块Q,将小滑块P无初速度放在传送带E端,要使小滑块能通过A点,传送带DE段至少为9m.
| 1 |
| 2 |
| v | 2 0 |
解得:v0=
| gR |
| 2 |
P、Q在D处发生弹性碰撞,由动量守恒和能量守恒得:
m1v0=m1v1+m2v2
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:v1=-
| 2 |
| 2 |
即碰撞刚结束P的瞬时速度为
| 2 |
(2)小滑块Q做匀减速运动至停止时距离最大,由动能定理得:
-μm2gx=-
| 1 |
| 2 |
向右运动的距离最大为x=0.8m,运动时间为t=
| 2x |
| v2 |
| 2×0.8 | ||
2
|
| 2 |
则:x相=vt+
| 1 |
| 2 |
(3)小滑块P恰能通过A点,由向心力公式得:m1g=m1
| ||
| R |
小滑块P从D到A,由动能定理得:-2m1gR=
| 1 |
| 2 |
| 1 |
| 2 |
则:vD=
| 5gR |
| 10 |
| 2 |
则P一直在传送带DE段加速,且末速度恰为3
| 10 |
由动能定理得:μm1gx′=
| 1 |
| 2 |
传送带至少为:x′=
| ||
| 2μg |
答:
(1)小滑块P从C处无初速度滑下,到轨道底端D碰撞刚结束的瞬间速度为
| 2 |
(2)小滑块Q第一次碰撞后向右运动的最大距离为6.4m,此过程产生的热量为12.8J.
(3)移走小滑块Q,将小滑块P无初速度放在传送带E端,要使小滑块能通过A点,传送带DE段至少为9m.
点评:解决本题的关键能够熟练运用机械能守恒定律,掌握摩擦产生热量的功能关系式Q=fx相,以及知道通过N点的临界情况是轨道的弹力为零,重力沿半径方向的分力提供向心力.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 如图所示,传送带以v为10m/s的速度向左匀速运行,BC段长L为2m,半径R为1.8m的光滑圆弧槽在B点与水平传送带相切.质量m为0.2kg的小滑块与传送带间的动摩擦因数μ为0.5,g取10m/s2,不计小滑块通过连接处的能量损失.求:
如图所示,传送带以v为10m/s的速度向左匀速运行,BC段长L为2m,半径R为1.8m的光滑圆弧槽在B点与水平传送带相切.质量m为0.2kg的小滑块与传送带间的动摩擦因数μ为0.5,g取10m/s2,不计小滑块通过连接处的能量损失.求: 如图所示,传送带以v=10m/s的速度逆时针运动,与水平面夹角θ=37°,传送带A 端到B 端距离L=29m.在传送带顶部A 端静止释放一小物体,物体与传送带间动摩擦因数 μ=0.5,g=10m/s2.试求物体从A 运动到底部B的时间 tAB.
如图所示,传送带以v=10m/s的速度逆时针运动,与水平面夹角θ=37°,传送带A 端到B 端距离L=29m.在传送带顶部A 端静止释放一小物体,物体与传送带间动摩擦因数 μ=0.5,g=10m/s2.试求物体从A 运动到底部B的时间 tAB.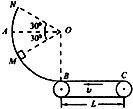 如图所示,传送带以v为10m/s速度向左匀速运行,BC段长L为2m,半径R为1.8m的光滑圆弧槽在B点与水平传送带相切,质量m为0.2kg的小滑块与传送带间的动摩擦因数μ为0.5,g取10m/s2,不计小滑块通过连接处的能量损失,求:(1)小滑块从M处无初速度滑下,到达底端B时的速度;(2)小滑块从M处无初速度滑下后,在传送带向右运少为多长?
如图所示,传送带以v为10m/s速度向左匀速运行,BC段长L为2m,半径R为1.8m的光滑圆弧槽在B点与水平传送带相切,质量m为0.2kg的小滑块与传送带间的动摩擦因数μ为0.5,g取10m/s2,不计小滑块通过连接处的能量损失,求:(1)小滑块从M处无初速度滑下,到达底端B时的速度;(2)小滑块从M处无初速度滑下后,在传送带向右运少为多长? 。
。