��Ŀ����
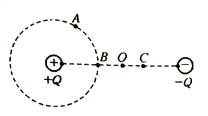
����Ŀ����ͼ��ʾ������m1=3kg�Ļ���C������Ϊ�ʵ㣩�����ڹ⻬��ƽ̨�ϣ���һ������Ȼ���ȵĵ��ɽӴ�����������������һ�˹̶�����ֱǽ���ϣ�ƽ̨�Ҳ��ˮƽ�����Ͻ���ƽ̨�����ŷ�������ľ��A��B����֪ľ��A��B�ij��Ⱦ�ΪL=5m��������Ϊm2=1��5kg��ľ��A��B�ϱ�����ƽ̨��ƽ��ľ��A��ƽ̨��ľ��B���Ӵ�����ճ��������C��ľ��A��B��Ķ�Ħ������Ϊ��1=0.3��ľ��A��B������Ķ�Ħ��������2=0.1������һˮƽ������������ڻ���C�ϣ������ɴ�ԭ����ʼ������ѹ��һ�ξ��룬Ȼ����C�ɾ�ֹ�ͷţ�������C�ջ���ľ��Aʱ������C���ٶ�Ϊ7m/s�������Ħ�����뻬��Ħ������С��ȣ�ȡg=10m/s2����

(1)���ɵ���������ܣ�
(2)����C�ջ���ľ��Aʱ��ľ��A��B������C�ļ��ٶȣ�
(3)�ӻ���C����ľ��A������ϵͳֹͣ�˶������ʱ�䣮
���𰸡���1��73��5J����2��3m/s2��1m/s2����3��4s
�������������������1��EPmax=![]() =73��5J
=73��5J
��2���軬��C��ľ��A�ϻ���ʱ������C�ļ��ٶ�Ϊa1��ľ��A��B�ļ��ٶ�Ϊa2������1m1g=m1a1��
��ã�a1=3m/s2��
��1m1g����2��m1+2m2��g=2m2a2��
��ã�a2=1m/s2��
��3���軬��C��ľ��A���˶���ʱ��Ϊt1�����ɣ� L=��v0t1��![]() a1t12��-
a1t12��-![]() a2t12
a2t12
��ã�t1=1s��t1=2��5s����ȥ��
�軬��C�뿪ľ��Aʱ���ٶ�ΪvC��ľ��A��B���ٶȷֱ�ΪvA��vB��
vC=v0��a1t1=4m/s
vA=vB=a2t1=1m/s
����C��ľ��B�ϻ���ʱ������C�ļ��ٶ�Ϊa1����B�ļ��ٶ�Ϊa3��
��1m1g����2��m1+m2��g=m2a3��
��ã�a3=3m/s2��
�辭��ʱ��t2��B��C�ﵽ��ͬ�ٶ�v�����У�v=vC��a1t2=vB+a3t2��
���t2=0��5s��v=2��5m/s
�ӻ���C����ľ��B����ľ��B�ٶ���ͬ�Ĺ����У�����C��ľ��B�����λ��Ϊ��
��x=![]() =0��75m��5m
=0��75m��5m
��֪�˹�����Cδ�뿪B��������1����2��B��C���ٺ�������˶�����B��Cһ���ȼ����˶��ļ��ٶ�Ϊa���˶�ʱ��Ϊt3��
��2��m1+m2��g=��m1+m2��a��
a=1m/s2��
0=v��at3��
t3=2��5s
��ӻ���C����ľ��A������ϵͳֹͣ�˶������ʱ��Ϊ�� t=t1+t2+t3=4s