题目内容
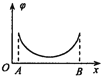
【题目】如图所示，AB是半径为R的四分之一光滑圆弧轨道，固定在竖直平面内，B为轨道最低点，距水平地面的高度为
。现将质量为m的小球从A点正上方的某点P（图中末画出）由静止释放，最后落在水平地面上的C点，C点距B点的水平距离为2R。重力加速度为g，不计空气阻力，求：
(1)小球经过B点时，轨道对小球的作用力大小；
(2)P点距A点的高度。
【答案】（1）
（2）
【解析】
小球从B点飞出做平抛运动，根据运动学规律求出B点的速度，在B点由牛顿第二定律求出轨道对小球的作用力大小；小球从P点落下至B点过程由动能定理求出P点距A点的高度；
解：(1)设小球在B点的速度大小为
，受到轨道的作用力大小为N，从过B点至落地过程的时间为t
由运动学规律： 
牛顿第二定律： 
联立以上各式得：
(2)设P点距A点的高度为h，小球从P点落下至B点过程由动能定理：
解得：
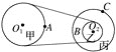
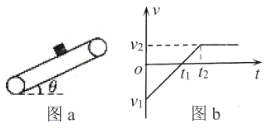
【题目】（6分）某物理小组的同学设计了一个粗制玩具小车通过凹形桥最低点时的速度的实验。所用器材有：玩具小车、压力式托盘秤、凹形桥模拟器（圆弧部分的半径为R=0.20m）。
完成下列填空：
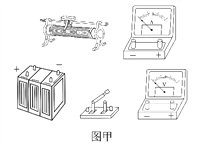
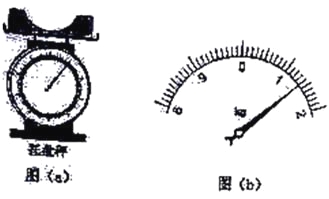
（1）将凹形桥模拟器静置于托盘秤上，如图（a）所示，托盘秤的示数为1.00kg；
（2）将玩具小车静置于凹形桥模拟器最低点时，托盘秤的示数如图（b）所示，该示数为_____kg;
（3）将小车从凹形桥模拟器某一位置释放，小车经过最低点后滑向另一侧，此过程中托盘秤的最大示数为m；多次从同一位置释放小车，记录各次的m值如下表所示：
序号 | 1 | 2 | 3 | 4 | 5 |
m（kg） | 1.80 | 1.75 | 1.85 | 1.75 | 1.90 |
（4）根据以上数据，可求出小车经过凹形桥最低点时对桥的压力为_____N；小车通过最低点时的速度大小为_______m/s。（重力加速度大小取9.80m/s2 ，计算结果保留2位有效数字）
