题目内容
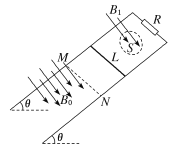
【题目】如图所示,两条相距L的光滑平行金属导轨倾斜放置,与水平面的夹角为θ,其上端接一阻值为R的电阻;一根与导轨垂直的金属棒置于两导轨上,金属棒的长度为L;在电阻、导轨和金属棒中间有一面积为S的区域,区域中存在垂直于导轨平面向下的均匀磁场,磁感应强度大小B1随时间t的变化关系为B1=kt,式中k为常量;虚线MN左侧是一匀强磁场区域,区域上边界MN(虚线)与导轨垂直,磁场的磁感应强度大小为B0,方问向也垂直于导轨平面向下。某时刻,金属棒从图示位置由静止释放,在t0时刻恰好以速度v0越过MN,此后沿导轨向下做匀速运动。金属棒与导轨始终相互垂直并接触良好,它们的电阻均忽略不计。
(1)分别求出在时刻t1(t1<t0)和时刻t2(t2>t0)的感应电流的大小;
(2)求金属棒的质量及0~t(t>t0)时间内电阻R产生的热量。
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]()
【解析】
(1)当![]() 时,金属棒未到达
时,金属棒未到达![]() ,由法拉第电磁感应定律有
,由法拉第电磁感应定律有
![]()
由欧姆定律得
![]()
解得
![]()
当![]() 时,金属棒已越过
时,金属棒已越过![]() ,金属棒切割磁感线产生的感应电动势
,金属棒切割磁感线产生的感应电动势
![]()
总感应电动势
![]()
由欧姆定律得
![]()
(2)当![]() 时,金属棒已越过
时,金属棒已越过![]() 做匀速直线运动,有
做匀速直线运动,有
![]()
解得
![]()
在![]() 时间内,电阻R产生的热量为
时间内,电阻R产生的热量为
![]()
在![]() 时间内,电阻R产生的热量为
时间内,电阻R产生的热量为
![]()
![]()

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目