题目内容
【题目】如图所示,质量为0.5kg的小杯里盛有1kg的水,用绳子系住小杯在竖直平面内做“水流星”表演,转动半径为1m , 小杯通过最高点的速度为4m/s , g取10m/s2 , 求: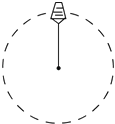
(1)在最高点时,绳的拉力?
(2)在最高点时水对小杯底的压力?
(3)为使小杯经过最高点时水不流出,在最高点时最小速率是多少?
【答案】
(1)
小杯质量m=0.5kg,水的质量M=1kg,在最高点时,杯和水的受重力和拉力作用,如图所示,
合力为:F合=(M+m)g+T…①
圆周半径为R,则有:F向=(M+m) ![]() …②
…②
F合提供向心力,有:(M+m)g+T=(M+m) ![]()
所以细绳拉力为:T=(M+m)( ![]() ﹣g)=(1+0.5)(
﹣g)=(1+0.5)( ![]() ﹣10)=9N,方向竖直向下
﹣10)=9N,方向竖直向下
(2)
在最高点时,水受重力Mg和杯的压力F作用,如图所示,
合力为:F合=Mg+F
圆周半径为R,则有:F向=M ![]()
F合提供向心力,有:Mg+F=M ![]()
所以杯对水的压力为:F=M( ![]() ﹣g)=1×(
﹣g)=1×( ![]() ﹣10)=6N;
﹣10)=6N;
根据牛顿第三定律,水对小杯底的压力为6N,方向竖直向上
(3)
小杯经过最高点时水恰好不流出时,此时杯对水的压力为零,只有水的重力作为向心力,由(2)得:
Mg=M ![]()
解得:v== ![]() =
= ![]() m/s
m/s
【解析】(1)小杯质量m=0.5kg , 水的质量M=1kg , 在最高点时,杯和水的受重力和拉力作用,如图所示,
合力为:F合=(M+m)g+T…①
圆周半径为R,则有:F向=(M+m) ![]() …②
…②
F合提供向心力,有:(M+m)g+T=(M+m) ![]()
所以细绳拉力为:T=(M+m)(![]() ﹣g)=(1+0.5)(
﹣g)=(1+0.5)(![]() ﹣10)=9N,方向竖直向下;(2)在最高点时,水受重力Mg和杯的压力F作用,如图所示,
﹣10)=9N,方向竖直向下;(2)在最高点时,水受重力Mg和杯的压力F作用,如图所示,
合力为:F合=Mg+F
圆周半径为R,则有:F向=M![]()
F合提供向心力,有:Mg+F=M![]()
所以杯对水的压力为:F=M(![]() ﹣g)=1×(
﹣g)=1×( ![]() ﹣10)=6N;
﹣10)=6N;
根据牛顿第三定律,水对小杯底的压力为6N , 方向竖直向上.(3)小杯经过最高点时水恰好不流出时,此时杯对水的压力为零,只有水的重力作为向心力,由(2)得:
Mg=M![]()
解得:v== ![]() =
= ![]() m/s
m/s
答:(1)在最高点时,绳的拉力为9N,方向竖直向下;(2)在最高点时水对小杯底的压力为6N,方向竖直向上;(3)在最高点时最小速率为 ![]() m/s
m/s![]()
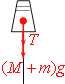

 出彩同步大试卷系列答案
出彩同步大试卷系列答案