题目内容
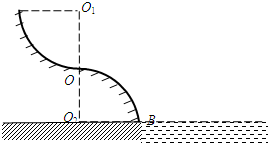 (2012?安徽一模)如图所示,AOB是游乐场中的滑道模型,它位于竖直平面内,由两个半径都是R的
(2012?安徽一模)如图所示,AOB是游乐场中的滑道模型,它位于竖直平面内,由两个半径都是R的| 1 | 4 |
(1)假设小滑块由A点静止下滑,求小滑块滑到O点时对O点的压力;
(2)凡能在O点脱离滑道的小滑块,其落水点到O2的距离如何;
(3)若小滑块从开始下滑到脱离滑道过程中,在两个圆弧上滑过的弧长相等,则小滑块开始下滑时应在圆弧AO上的何处(用该处到O1点的连线与竖直线的夹角的三角函数值表示).
分析:(1)对从A到O的运动过程中运用动能定理及向心力公式即可解题;
(2)凡能在O点脱离滑道的小滑块,离开轨道后做平抛运动,先求出最小速度,再根据平抛运动的规律即可求解;
(3)如图所示,设滑块出发点为P1,离开点为P2,按题意要求O1P1、O2P2与竖直方向的夹角相等,设其为θ,若离开滑道时的速度为v,则滑块在P2处脱离滑道的条件是
=mgcosθ,结合机械能守恒即可求解.
(2)凡能在O点脱离滑道的小滑块,离开轨道后做平抛运动,先求出最小速度,再根据平抛运动的规律即可求解;
(3)如图所示,设滑块出发点为P1,离开点为P2,按题意要求O1P1、O2P2与竖直方向的夹角相等,设其为θ,若离开滑道时的速度为v,则滑块在P2处脱离滑道的条件是
| mv2 |
| R |
解答: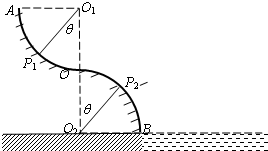 解:(1)从A到O的运动过程中根据动能定理得:
解:(1)从A到O的运动过程中根据动能定理得:
mgR=
mv2
根据向心力公式得:
Fn-mg=m
联立得:Fn=3mg
由牛顿第三定律得:压力大小为3mg,方向竖直向下.
(2)从A点下滑的滑块到O点的速度为
,设能脱离轨道的最小速度为v1
则有:mg=m
,得:v1=
R=
gt2 X=vot
联立得:
R≤x≤2R
(3)如图所示,设滑块出发点为P1,离开点为P2,按题意要求O1P1、O2P2与竖直方向的夹角相等,
设其为θ,若离开滑道时的速度为v,则滑块在P2处脱离滑道的条件是
=mgcosθ
由机械能守恒 2mgR(1-cosθ)=
mv2
联立解得 cosθ=
答:(1)小滑块滑到O点时对O点的压力大小为3mg,方向竖直向下;
(2)凡能在O点脱离滑道的小滑块,其落水点到O2的距离范围为
R≤x≤2R;
(3)若小滑块从开始下滑到脱离滑道过程中,在两个圆弧上滑过的弧长相等,则小滑块开始下滑时应在圆弧AO上的cosθ=
处.
 解:(1)从A到O的运动过程中根据动能定理得:
解:(1)从A到O的运动过程中根据动能定理得:mgR=
| 1 |
| 2 |
根据向心力公式得:
Fn-mg=m
| v2 |
| R |
联立得:Fn=3mg
由牛顿第三定律得:压力大小为3mg,方向竖直向下.
(2)从A点下滑的滑块到O点的速度为
| 2gR |
则有:mg=m
| v12 |
| R |
| gR |
R=
| 1 |
| 2 |
联立得:
| 2 |
(3)如图所示,设滑块出发点为P1,离开点为P2,按题意要求O1P1、O2P2与竖直方向的夹角相等,
设其为θ,若离开滑道时的速度为v,则滑块在P2处脱离滑道的条件是
| mv2 |
| R |
由机械能守恒 2mgR(1-cosθ)=
| 1 |
| 2 |
联立解得 cosθ=
| 4 |
| 5 |
答:(1)小滑块滑到O点时对O点的压力大小为3mg,方向竖直向下;
(2)凡能在O点脱离滑道的小滑块,其落水点到O2的距离范围为
| 2 |
(3)若小滑块从开始下滑到脱离滑道过程中,在两个圆弧上滑过的弧长相等,则小滑块开始下滑时应在圆弧AO上的cosθ=
| 4 |
| 5 |
点评:该题主要考查了动能定理、向心力公式、平抛运动的规律及机械能守恒定律,综合性较强,难度较大.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
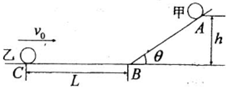 (2012?安徽一模)如图所示,水平面与斜面由光滑的小圆弧相连,一光滑小球甲从倾角θ=30°的斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0沿水平向右运动,甲释放后经过t=1s在水平面上刚好与乙相碰.已知C点与斜面底端B处的距离L=3.8m,小球乙与水平面的动摩擦因数μ=0.2,求乙的速度v0.(g=10m/s2)
(2012?安徽一模)如图所示,水平面与斜面由光滑的小圆弧相连,一光滑小球甲从倾角θ=30°的斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0沿水平向右运动,甲释放后经过t=1s在水平面上刚好与乙相碰.已知C点与斜面底端B处的距离L=3.8m,小球乙与水平面的动摩擦因数μ=0.2,求乙的速度v0.(g=10m/s2)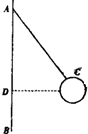 (2012?安徽一模)在“用圆锥摆实验验证向心力公式“的实验中,AB为竖直转轴,细绳一端系在A点,另一端与小球C相连,如图所示.当转轴转动时,C球在水平面内做匀速圆周运动.实验步骤如下:
(2012?安徽一模)在“用圆锥摆实验验证向心力公式“的实验中,AB为竖直转轴,细绳一端系在A点,另一端与小球C相连,如图所示.当转轴转动时,C球在水平面内做匀速圆周运动.实验步骤如下: