题目内容
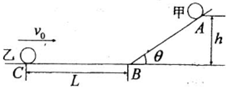 (2012?安徽一模)如图所示,水平面与斜面由光滑的小圆弧相连,一光滑小球甲从倾角θ=30°的斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0沿水平向右运动,甲释放后经过t=1s在水平面上刚好与乙相碰.已知C点与斜面底端B处的距离L=3.8m,小球乙与水平面的动摩擦因数μ=0.2,求乙的速度v0.(g=10m/s2)
(2012?安徽一模)如图所示,水平面与斜面由光滑的小圆弧相连,一光滑小球甲从倾角θ=30°的斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0沿水平向右运动,甲释放后经过t=1s在水平面上刚好与乙相碰.已知C点与斜面底端B处的距离L=3.8m,小球乙与水平面的动摩擦因数μ=0.2,求乙的速度v0.(g=10m/s2)分析:根据牛顿第二定律和运动学公式求出甲球在斜面上运动的时间,以及运动到B处时的速度,甲球在水平面上做匀速直线运动,乙球在水平面上做匀减速运动,两者位移之和等于L,根据牛顿第二定律和位移公式求解乙的速度v0.
解答:解:设小球甲在光滑斜面上运动的加速度为a1,运动时间为t1,运动到B处时的速度为v1,从B处到与小球乙相碰所用时间为t2,则
由牛顿第二定律得
mgsin30°=ma1,得到a1=gsin30°=5m/s2
由
=
a1
得,t1=
=0.2s
则t2=t-t1=0.8s,v1=a1t1=1m/s
乙球运动的加速度为a2=
=μg=2m/s2
根据位移关系得
v0t-
a2t2+v1t2=L
代入解得v0=4m/s
答:乙的速度v0=4m/s.
由牛顿第二定律得
mgsin30°=ma1,得到a1=gsin30°=5m/s2
由
| h |
| sin30° |
| 1 |
| 2 |
| t | 2 1 |
|
则t2=t-t1=0.8s,v1=a1t1=1m/s
乙球运动的加速度为a2=
| μmg |
| m |
根据位移关系得
v0t-
| 1 |
| 2 |
代入解得v0=4m/s
答:乙的速度v0=4m/s.
点评:本题是相遇问题,在分析两个小球运动的基础上,研究两者之间的关系是关键.此题要注意甲球是光滑的,在水平面上做匀速直线运动,不是匀减速运动.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
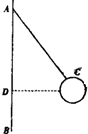 (2012?安徽一模)在“用圆锥摆实验验证向心力公式“的实验中,AB为竖直转轴,细绳一端系在A点,另一端与小球C相连,如图所示.当转轴转动时,C球在水平面内做匀速圆周运动.实验步骤如下:
(2012?安徽一模)在“用圆锥摆实验验证向心力公式“的实验中,AB为竖直转轴,细绳一端系在A点,另一端与小球C相连,如图所示.当转轴转动时,C球在水平面内做匀速圆周运动.实验步骤如下: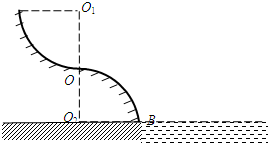 (2012?安徽一模)如图所示,AOB是游乐场中的滑道模型,它位于竖直平面内,由两个半径都是R的
(2012?安徽一模)如图所示,AOB是游乐场中的滑道模型,它位于竖直平面内,由两个半径都是R的