题目内容
将一个质量为1kg的小球从某高处以3m/s的初速度水平抛出,测得小球落地点到抛出点的水平距离为1.2m.小球运动中所受空气阻力忽略不计,g=10m/s2.求:
(1)小球在空中运动的时间;
(2)抛出点距地面的高度;
(3)小球落地时重力的瞬时功率.
(1)小球在空中运动的时间;
(2)抛出点距地面的高度;
(3)小球落地时重力的瞬时功率.
分析:平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据水平位移和初速度求出运动的时间,根据h=
gt2球出下落的高度.根据P=mgvcosθ=mgvy求出重力的瞬时功率.
| 1 |
| 2 |
解答:解:(1)小球在水平方向上做匀速直线运动,根据t=
得,
解得小球在空中运动的时间t=0.4s
(2)小球在竖直方向上做自由落体运动,根据h=
gt2
解得抛出点距地面的高度h=0.8m
(3)小球落地前竖直分速度vy=gt=4m/s
重力的瞬时功率PG=mg vy=40W.
答:(1)小球在空中运动的时间为0.4s.
(2)抛出点距地面的高度为0.8m.
(3)小球落地时重力的瞬时功率为40W.
| x |
| v0 |
解得小球在空中运动的时间t=0.4s
(2)小球在竖直方向上做自由落体运动,根据h=
| 1 |
| 2 |
解得抛出点距地面的高度h=0.8m
(3)小球落地前竖直分速度vy=gt=4m/s
重力的瞬时功率PG=mg vy=40W.
答:(1)小球在空中运动的时间为0.4s.
(2)抛出点距地面的高度为0.8m.
(3)小球落地时重力的瞬时功率为40W.
点评:解决本题的关键掌握平抛运动在水平方向上和竖直方向上的运动规律,以及掌握瞬时功率的公式P=Fvcosθ.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
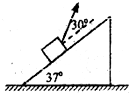 将一个质量为1kg的物块置于倾角为37°的固定斜面上,物块在与斜面夹角为30°的拉力F作用下加速上升,已知物块与斜面间的动摩擦因数为0.2,F大小为10N,则物块上升的加速度约为:(sin37°=0.6,cos37°=0.8,sin30°=0.5,cos30°=0.866)( )
将一个质量为1kg的物块置于倾角为37°的固定斜面上,物块在与斜面夹角为30°的拉力F作用下加速上升,已知物块与斜面间的动摩擦因数为0.2,F大小为10N,则物块上升的加速度约为:(sin37°=0.6,cos37°=0.8,sin30°=0.5,cos30°=0.866)( )| A、1.6m/s2 | B、1m/s2 | C、2m/s2 | D、8m/s2 |
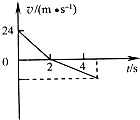 将一个质量为1kg的小球竖直向上抛出,最终落回抛出点,运动过程中所受阻力大小恒定,方向与运动方向相反.该过程的v-t图象如图所示,g取10m/s2.下列说法中正确的是( )
将一个质量为1kg的小球竖直向上抛出,最终落回抛出点,运动过程中所受阻力大小恒定,方向与运动方向相反.该过程的v-t图象如图所示,g取10m/s2.下列说法中正确的是( )| A、小球上升与下落所用时间之比为2:3 | B、小球下落过程,处于失重状态 | C、小球上升过程中克服阻力做功48J | D、小球上升过程中机械能的损失大于下落过程中的机械能损失 |
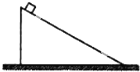 如图所示,将一个质量为1kg的小物块轻轻放在倾角为37°(sin37°=0.6)的斜面上,已知斜面质量也为1kg,重力加速度为10m/s2.若斜面在足够粗糙的水平地面上没有滑动,那么地面的支持力FN和摩擦力Ff有可能为( )
如图所示,将一个质量为1kg的小物块轻轻放在倾角为37°(sin37°=0.6)的斜面上,已知斜面质量也为1kg,重力加速度为10m/s2.若斜面在足够粗糙的水平地面上没有滑动,那么地面的支持力FN和摩擦力Ff有可能为( )| A、FN=16.4N,Ff=4.8N | B、FN=18.2N,Ff=2.4N | C、FN=20N,Ff=0 | D、FN=20N,Ff=4.8N |
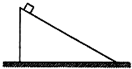 如图所示,将一个质量为1kg的小物块轻轻放上倾角为37°(sin37°=0.6)的斜面,已知斜面质量也为1kg,重力加速度为l0m/s2.斜面放在足够粗糙的水平地面上没有滑动,那么地面对斜面的支持力N和摩擦力f有可能为( )
如图所示,将一个质量为1kg的小物块轻轻放上倾角为37°(sin37°=0.6)的斜面,已知斜面质量也为1kg,重力加速度为l0m/s2.斜面放在足够粗糙的水平地面上没有滑动,那么地面对斜面的支持力N和摩擦力f有可能为( )