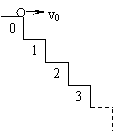题目内容
 如图所示,阶梯的每个台阶的宽和高都是0.1m,若要使小球能落到第9台阶上,则初始水平速度范围为
如图所示,阶梯的每个台阶的宽和高都是0.1m,若要使小球能落到第9台阶上,则初始水平速度范围为2m/s<v<
m/s
3
| ||
| 2 |
2m/s<v<
m/s
(g取10m/s2)3
| ||
| 2 |
分析:一球以水平速度由第0级台阶上抛出欲打在第9级台阶上,求出两个临界情况,速度最小时打在第8级台阶的边缘上,速度最大时,打在第9级台阶的边缘上.根据h=
gt2和x=vt,得出v的临界值.
| 1 |
| 2 |
解答:解:若小球打在第8级台阶的边缘上,则h1=8×0.1m=0.8m
根据h1=
gt12得,t1=
=0.4s
此时的初速度v1=
=
m/s=2m/s.
若小球打在第9级台阶的边缘上,则h2=9×0.1=0.9m.
根据h2=
gt22得,t2=
=
s=
s.
此时的初速度v2=
=
m/s=
m/s.
所以初始速度的范围2m/s<v<
m/s.
故答案为:2m/s<v<
m/s
根据h1=
| 1 |
| 2 |
|
此时的初速度v1=
| x |
| t |
| 0.1×8 |
| 0.4 |
若小球打在第9级台阶的边缘上,则h2=9×0.1=0.9m.
根据h2=
| 1 |
| 2 |
|
|
3
| ||
| 10 |
此时的初速度v2=
| x2 |
| t2 |
| 0.9 | ||||
|
3
| ||
| 2 |
所以初始速度的范围2m/s<v<
3
| ||
| 2 |
故答案为:2m/s<v<
3
| ||
| 2 |
点评:解决本题的关键掌握临界情况,结合平抛运动水平方向和竖直方向上的运动规律进行求解.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图所示,内壁光滑的直角细管轨道ABC竖直放置,BC边水平,一小球从A端由静止释放,沿ABC轨道运动到C点,现将此轨道改制成一个内壁光滑的直角阶梯轨道ADEC,每个阶梯的一直角边水平且不超过AC边界,仍将小球从A端由静止释放,沿ADEC运动到C点,设所有轨道转弯处由一极小的光滑圆弧连接,小球通过拐弯处无动能损失,拐弯时间忽略不计,则( )
如图所示,内壁光滑的直角细管轨道ABC竖直放置,BC边水平,一小球从A端由静止释放,沿ABC轨道运动到C点,现将此轨道改制成一个内壁光滑的直角阶梯轨道ADEC,每个阶梯的一直角边水平且不超过AC边界,仍将小球从A端由静止释放,沿ADEC运动到C点,设所有轨道转弯处由一极小的光滑圆弧连接,小球通过拐弯处无动能损失,拐弯时间忽略不计,则( )