题目内容
8.某同学设计了一个如图1所示的装置来测定滑块与木板间的动摩擦因数,装置水平放置,其中A为滑块,B和C是质量可调的砝码,不计绳和滑轮的质量及它们之间的摩擦.实验中该同学在砝码总质量(m+m′=m0)保持不变的条件下,改变m和m′的大小,测出不同m下系统的加速度,然后通过实验数据的分析就可求出滑块与木板间的动摩擦因数.
(1)该同学手中有打点计时器、纸带、10个质量均为100克的砝码、滑块、一端带有定滑轮的长木板、细线,为了完成本实验,得到所要测量的物理量,还应有BD
A.秒表 B.毫米刻度尺 C.天平 D.低压交流电源
(2)实验中,该同学得到一条较为理想的纸带,如图3所示,从清晰的O点开始,每隔4个点取一计数点(中间4个点没画出),分别记为A、B、C、D、E、F,各计数点到O点的距离为OA=1.61cm,OB=4.02cm,OC=7.26cm,OD=l1.30cm,OE=16.14cm,OF=21.80cm,打点计时器打点频率为50Hz,则由此纸带可得到打E点时滑块的速度v=0.53m/s,此次实验滑块的加速度a=0.81m/s2.(结果均保留两位有效数字)
(3)在实验数据处理中,该同学以m为横轴,以系统的加速度a为纵轴,绘制了如图2所示的实验图线,结合本实验可知滑块与木板间的动摩擦因数μ=0.30.g取1Om/s2)
分析 (1)本实验中打点计时器需要交流电源,测量纸带各点距离需要长度的测量工具刻度尺.
(2)每隔4个点取一计数点,相邻计数点之间的时间间隔为0.1s,由匀加速规律可得,用平均速度等于中间时刻的瞬时速度求解E点速度、用△x=at2求解加速度.特别注意有效数字保留2位即可;
(3)对系统应用牛顿第二定律,得到图线的纵轴截距为-μg,可解得动摩擦因数.
解答 解:(1)A、打点计时器通过打点即可知道时间,故不需要秒表测时间,A错误.
B、实验需要测量两点之间的距离,故需要毫米刻度尺,B正确.
C、本实验中可以不测滑块的质量,而且砝码的质量已知,故不需要天平,C错误.
D、打点计时器要用到低压交流电源才能工作,D正确.
故选:BD
(2)每隔4个点取一计数点,相邻计数点之间的时间间隔为0.1s,故用平均速度等于中间时刻的瞬时速度可得:
${v}_{E}=\frac{OF-OD}{2T}=0.53m/s$
由△x=at2可得
$a=\frac{CF-OC}{(3T)^{2}}=0.81m/{s}^{2}$
(3)对ABC系统应用牛顿第二定律可得$a=\frac{mg-μ(m+m′)g}{m+{m}_{0}}=\frac{(1+μ)mg}{m+{m}_{0}}$
所以,a-t图象中,纵轴的截距为-μg,故-μg=-3,解得μ=0.30
故答案为:(1)BD (2)0.53;0.81 (3)0.30
点评 熟悉纸带的处理方法,中间位置的速度用平均速度求,加速度用推导式用△x=at2,注意时间的数值和长度的单位、逐差法等;对于图象问题,注意分析截距、斜率、面积等的含义,找出有用的数据.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
18. 如图所示,甲、乙两辆同型号的轿车,它们外形尺寸如下表所示.正在通过十字路口的甲车正常匀速行驶,车速v甲=10m/s,车头距中心O的距离为20m,就在此时,乙车闯红灯匀速行驶,车头距中心O的距离为30m.
如图所示,甲、乙两辆同型号的轿车,它们外形尺寸如下表所示.正在通过十字路口的甲车正常匀速行驶,车速v甲=10m/s,车头距中心O的距离为20m,就在此时,乙车闯红灯匀速行驶,车头距中心O的距离为30m.
(1)求乙车的速度在什么范围之内,必定不会造成撞车事故.
(2)若乙的速度v乙=15m/s,司机的反应时间为0.5s,为了防止撞车事故发生,乙车刹车的加速度至少要多大?会发生撞车事故吗?
轿车外形尺寸及安全技术参数
 如图所示,甲、乙两辆同型号的轿车,它们外形尺寸如下表所示.正在通过十字路口的甲车正常匀速行驶,车速v甲=10m/s,车头距中心O的距离为20m,就在此时,乙车闯红灯匀速行驶,车头距中心O的距离为30m.
如图所示,甲、乙两辆同型号的轿车,它们外形尺寸如下表所示.正在通过十字路口的甲车正常匀速行驶,车速v甲=10m/s,车头距中心O的距离为20m,就在此时,乙车闯红灯匀速行驶,车头距中心O的距离为30m.(1)求乙车的速度在什么范围之内,必定不会造成撞车事故.
(2)若乙的速度v乙=15m/s,司机的反应时间为0.5s,为了防止撞车事故发生,乙车刹车的加速度至少要多大?会发生撞车事故吗?
轿车外形尺寸及安全技术参数
| 长l/mm | 宽b/mm | 高h/mm | 最大速度km/h | 急刹车加速度m/s2 |
| 3896 | 1650 | 1465 | 144 | -4~-6 |
16.两个共点力的合力与分力的关系是( )
| A. | 合力大小一定等于两个分力大小之和 | |
| B. | 合力大小一定大于两个分力大小之和 | |
| C. | 合力大小一定大于一个分力的大小,小于另一个分力的大小 | |
| D. | 合力大小可能比两个分力的大小都大,可能都小,也可能比一个分力大,比另一个分力小 |
3.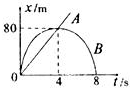 如图所示是A、B两质点从同一地点做直线运动的位移随时间变化的x-t图象,则下列说法中正确的是( )
如图所示是A、B两质点从同一地点做直线运动的位移随时间变化的x-t图象,则下列说法中正确的是( )
 如图所示是A、B两质点从同一地点做直线运动的位移随时间变化的x-t图象,则下列说法中正确的是( )
如图所示是A、B两质点从同一地点做直线运动的位移随时间变化的x-t图象,则下列说法中正确的是( )| A. | A质点做匀加速直线运动 | |
| B. | A、B两质点在8s末相遇 | |
| C. | B质点最初4s做减速运动,后4s做加速运动 | |
| D. | B质点先沿负方向做直线运动,后沿正方向做直线运动 |
13. 如图所示,图线a是某一电源的U-I曲线,图线b是一定值电阻的U-I曲线.若将该电源与该定值电阻连成闭合电路(已知该电源的内阻r=2.0Ω),则下列说法错误的是( )
如图所示,图线a是某一电源的U-I曲线,图线b是一定值电阻的U-I曲线.若将该电源与该定值电阻连成闭合电路(已知该电源的内阻r=2.0Ω),则下列说法错误的是( )
 如图所示,图线a是某一电源的U-I曲线,图线b是一定值电阻的U-I曲线.若将该电源与该定值电阻连成闭合电路(已知该电源的内阻r=2.0Ω),则下列说法错误的是( )
如图所示,图线a是某一电源的U-I曲线,图线b是一定值电阻的U-I曲线.若将该电源与该定值电阻连成闭合电路(已知该电源的内阻r=2.0Ω),则下列说法错误的是( )| A. | 将2只这种电阻串联作为外电阻,电源输出功率最大 | |
| B. | 将3只这种电阻并联作为外电阻,电源输出功率最大 | |
| C. | 该定值电阻为6Ω | |
| D. | 该电源的电动势为20V |
 某同学利用数字化信息系统研究一定质量理想气体的状态变化,实验后计算机屏幕显示如图所示的p-V图象.已知该气体在状态A时的温度为27℃.求:
某同学利用数字化信息系统研究一定质量理想气体的状态变化,实验后计算机屏幕显示如图所示的p-V图象.已知该气体在状态A时的温度为27℃.求: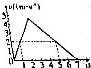 一质量m=0.1kg的小物块能止在粗糙的水平地面上,t=0时对物块施加一水平向右的拉力F,某时刻撤去拉力F,物块继续向右运动,其v-t图象如图所示.取g=10m/s2,求:
一质量m=0.1kg的小物块能止在粗糙的水平地面上,t=0时对物块施加一水平向右的拉力F,某时刻撤去拉力F,物块继续向右运动,其v-t图象如图所示.取g=10m/s2,求: