题目内容
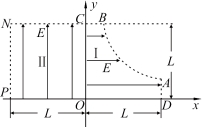
【题目】如图所示，宽度为
L的区域被平均分为区域Ⅰ、Ⅱ、Ⅲ，其中Ⅰ、Ⅲ有匀强磁场，他们的磁感应强度大小相等，方向垂直纸面且相反，长为L，宽为
的矩形abcd紧邻磁场下方，与磁场边界对齐，O为dc边中点，P为dc边中垂线上一点，OP=3L，矩形内有匀强电场，电场强度大小为E，方向由a指向O；电荷量为q，质量为m，重力不计的带电粒子由a点静止释放，经电场加速后进入磁场，运动轨迹刚好与区域Ⅲ的右边界相切；
（1）求该粒子经过O点的速度vo
（2）求匀强磁场的磁感应强度大小B
（3）若在AO之间距O点x处静止释放该粒子，粒子在磁场中共偏转n次到达P点，求x满足的条件及n的可能取值．
【答案】（1）
（2）
（3）
，其中n=2、3、4、5、6、7、8
【解析】
试题分析：
（1）由题意可知，ao=L，粒子在ao加速过程有：
得粒子经过O点时的速度大小为
（2）粒子在磁场区域Ⅲ中的运动轨迹如图；若粒子轨迹圆半径为R0，由几何关系可知
由洛伦兹力公式和牛顿第二定律可得：
（3）若粒子在磁场中一共经过n次偏转到达P点，设粒子轨迹圆半径为R，由几何关系可得：
，依题意有：0<R≤R0
解得：
，且n取正整数
设粒子在磁场中的运动速率为v，有
在电场中加速过程，由动能定理:qEx=
mv2
解得：，其中n=2、3、4、5、6、7、8
练习册系列答案
口算能手系列答案
相关题目
