题目内容
3.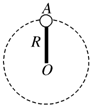 一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,如图所示,则下列说法正确的是( )
一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,如图所示,则下列说法正确的是( )| A. | 小球过最高点的最小速度是$\sqrt{gR}$ | |
| B. | 若v=$\sqrt{gR}$,小球过最高点时,杆对小球的弹力为mg | |
| C. | 若v<$\sqrt{gR}$,小球过最高点时,杆对球的作用力一定随速度增大而减小 | |
| D. | 若v>$\sqrt{gR}$,小球过最高点时,杆对小球的弹力竖直向上 |
分析 小球在最高点,杆子可以表现为支持力,也可以表现为拉力,在最高点的最小速度为零,根据牛顿第二定律分析杆子对小球的作用力随速度变化的关系.
解答 解:A、小球通过最高点的最小速度为零.故A错误.
B、当小球到达最高点弹力为零时,重力提供向心力,有mg=$m\frac{{v}^{2}}{R}$,解得v=$\sqrt{gR}$,即当速度v=$\sqrt{gR}$时,杆子所受的弹力为零.故B错误.
C、小球在最高点,若v<$\sqrt{gR}$,则有:$mg-F=m\frac{{v}^{2}}{R}$,杆子随着速度的增大而减小,故C正确;
D、若v>$\sqrt{gR}$,则重力不足以提供向心力,则杆子对球的作用力的方向竖直向下,故D错误.
故选:C.
点评 解决本题的关键知道小球做圆周运动向心力的来源,知道最高点的临界情况,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
6.嫦娥奔月蕴含着炎黄儿女千年的飞天梦想,随着我国“嫦娥计划”的逐步进展,奔月梦想即将成为现实.某校物理兴趣小组收集了月球表面的许多资料,如 ①没有空气;②重力加速度约为地球表面的l/6;③没有磁场…并设想登上月球后,完成如下实验:在空中从同一高度同时自由释放氢气球和铅球,忽略地球和其它星球的影响,你认为以下说法正确的是( )
| A. | 氢气球和铅球都处于漂浮状态 | |
| B. | 氢气球将加速上升,铅球加速下落 | |
| C. | 氢气球和铅球都将下落,且同时落地 | |
| D. | 氢气球和铅球都将下落,但铅球先落到地面 |
7.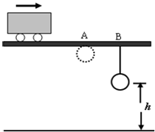 距地面高5m的水平直轨道A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小1O.可求得h等于( )
距地面高5m的水平直轨道A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小1O.可求得h等于( )
 距地面高5m的水平直轨道A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小1O.可求得h等于( )
距地面高5m的水平直轨道A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小1O.可求得h等于( )| A. | 4.75m | B. | 3.75m | C. | 2.25m | D. | 1.25m |
11.一个理想变压器原线圈和副线圈的匝数分别为n1和n2,正常工作时输入和输出的电压、电流、功率分别为U1和U2,I1和I2,P1和P2,已知n1>n2,则( )
| A. | U1>U2,P1<P2 | B. | P1<P2,I1<I2 | C. | I1<I2,U1>U2 | D. | P1>P2,I1>I2 |
18.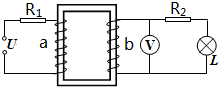 理想变压器原线圈a匝数为n1=400匝,副线圈b匝数n2=200匝,线圈a接在$u=44\sqrt{2}sin314t$V的交流电源上,“12V,6W”的灯泡恰好正常发光.电阻R2=16Ω,电压表V为理想电表.下列推断不正确的是( )
理想变压器原线圈a匝数为n1=400匝,副线圈b匝数n2=200匝,线圈a接在$u=44\sqrt{2}sin314t$V的交流电源上,“12V,6W”的灯泡恰好正常发光.电阻R2=16Ω,电压表V为理想电表.下列推断不正确的是( )
 理想变压器原线圈a匝数为n1=400匝,副线圈b匝数n2=200匝,线圈a接在$u=44\sqrt{2}sin314t$V的交流电源上,“12V,6W”的灯泡恰好正常发光.电阻R2=16Ω,电压表V为理想电表.下列推断不正确的是( )
理想变压器原线圈a匝数为n1=400匝,副线圈b匝数n2=200匝,线圈a接在$u=44\sqrt{2}sin314t$V的交流电源上,“12V,6W”的灯泡恰好正常发光.电阻R2=16Ω,电压表V为理想电表.下列推断不正确的是( )| A. | 电压表V的示数为22V | |
| B. | R1消耗的功率是1W | |
| C. | 交变电流的频率为50Hz | |
| D. | 穿过铁芯的磁通量的最大变化率为$\frac{{\sqrt{2}}}{10}Wb/s$ |
12.某拱桥可以看成是一段圆弧,当汽车以10m/s的速度通过桥顶时,对桥顶的压力为车重的$\frac{3}{4}$倍,要使汽车对桥顶恰好没有压力,汽车的速度应为( )(g=10m/s2)
| A. | 15m/s | B. | 20m/s | C. | 25m/s | D. | 30m/s |
13.下列有关质点的说法中,正确的是( )
| A. | 当研究地球的自转时,可以将其看做质点 | |
| B. | 用GPS定位系统确定正在南极冰盖考察的某科考队员的位置时,该队员可看做质点 | |
| C. | 研究乒乓球在空中飞旋的轨迹时,不能将其看做质点 | |
| D. | 凡是小的物体,皆可看成质点;凡是大的物体,皆不能看成质点 |