题目内容
16.如图甲所示,光滑的平行水平金属导轨MN、PQ相距L,在M点和P点间连接一个阻值为R的电阻,一质量为m、电阻为r、长度也刚好为L的导体棒ab垂直搁在导轨上,在导体棒的右侧导轨间加一有界匀强磁场,磁场方向垂直于导轨平面,宽度为d0,磁感应强度为B,设磁场左边界到导体棒的距离为d.现用一个水平向右的力F拉导体棒,使它由静止开始运动,棒离开磁场前已做匀速直线运动,与导轨始终保持良好接触,导轨电阻不计,水平力F与位移x的关系图象如图乙所示,F0已知.求: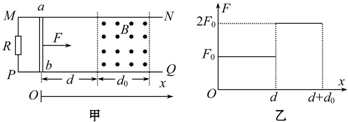
(1)导体棒ab离开磁场右边界时的速度.
(2)导体棒ab通过磁场区域的过程中整个回路所消耗的电能.
(3)d0满足什么条件时,导体棒ab进入磁场后一直做匀速运动?
分析 (1)由于导体棒离开时已经匀速运动,故安培力与外力F大小相等方向相反,据此可以求出棒离开磁场时的速度.
(2)克服安培力所做功等于回路中产生的热量即消耗的电能,根据动能定理可以正确求出.
(3)由题意可知导体棒运动到右端时已经匀速运动,因此只要导体棒进入磁场时的速度等于(1)中所求速度,棒ab进入磁场即可匀速运动,根据动能定理可以求出d0满足的条件.
解答 解:(1)设离开右边界时棒ab速度为υ,则有:
E=Blv…①
$I=\frac{E}{R+r}$…②
对棒有:2F0-BIl=0 ③
联立①③③解得:$V=\frac{2{F}_{0}(R+r)}{{B}^{2}{l}^{2}}$,
故棒ab离开磁场右边界时的速度为:$V=\frac{2{F}_{0}(R+r)}{{B}^{2}{l}^{2}}$.
(2)在ab棒运动的整个过程中,根据动能定理有:
${F}_{0}{d}_{0}+2{F}_{0}d-{W}_{安}=\frac{1}{2}m{V}^{2}-0$…④
由功能关系:E电=W安…⑤
联立④⑤解得:${E_电}={F_0}({d_0}+2d)-\frac{{2m{F_0}^2{{(R+r)}^2}}}{{{B^4}{l^4}}}$
故棒ab通过磁场区域的过程中整个回路所消耗的电能为:${E_电}={F_0}({d_0}+2d)-\frac{{2m{F_0}^2{{(R+r)}^2}}}{{{B^4}{l^4}}}$.
(3)设棒刚进入磁场时的速度为υ0,则有:
${F}_{0}{d}_{0}=\frac{1}{2}m{V}_{0}{\;}^{2}-0$
当υ0=υ,
故当d0满足满足条件为:${d_0}=\frac{{2{F_0}m{{(R+r)}^2}}}{{{B^4}{l^4}}}$时,进入磁场后一直匀速运动.
答:(1)导体棒ab离开磁场右边界时的速度为$\frac{2{F}_{0}(R+r)}{{B}^{2}{l}^{2}}$.
(2)导体棒ab通过磁场区域的过程中整个回路所消耗的电能为${F}_{0}({d}_{0}+2d)-\frac{2m{F}_{0}{\;}^{2}{(R+r)}^{2}}{{B}^{4}{l}^{4}}$.
(3)当d0满足满足条件为:${d_0}=\frac{{2{F_0}m{{(R+r)}^2}}}{{{B^4}{l^4}}}$时,进入磁场后一直匀速运动.
点评 本题考查了电磁感应与力学和功能关系的结合,对于这类问题一定要正确分析安培力的大小和方向然后根据运动状态列出牛顿第二定律方程求解,注意克服安培力所做的功等于整个回路消耗的电能即回路中产生的热量.

| A. | 1.9km/s | B. | 7.3km/s | C. | 7.9km/s | D. | 11.2km/s |
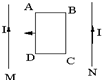 如图所示,在两根平行长直导线M、N中,通过同方向、同强度的电流,导线框ABCD和两导线在同一平面内.线框沿着与两导线垂直的方向,自右向左在两导线间匀速移动.在移动过程中,线框中产生感应电流的方向是( )
如图所示,在两根平行长直导线M、N中,通过同方向、同强度的电流,导线框ABCD和两导线在同一平面内.线框沿着与两导线垂直的方向,自右向左在两导线间匀速移动.在移动过程中,线框中产生感应电流的方向是( )| A. | 沿ADCBA,方向不变 | B. | 沿ABCDA,方向不变 | ||
| C. | 由沿ABCDA方向变成沿ADCBA方向 | D. | 由沿ADCBA方向变成沿ABCDA方向 |
| A. | 要使放在河中的纸船逐渐靠近河岸,可向比纸船更远处投掷石子形成水波 | |
| B. | 两个在水中潜泳并且靠得较近的运动员能听到对方发出的声音是声波在液体中传播的应用 | |
| C. | 光缆是利用机械波传递信息 | |
| D. | 宇航员在宇宙飞船里,击打船壁只能引起机械振动,不能形成声波 |
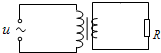 如图所示,理想变压器原、副线圈的匝数比为2:1,电阻R=55.0Ω,原线圈两端接一正弦式交变电流,电压u随时间t变化的规律为u=110$\sqrt{2}$sin20πt(V),时间t的单位是s.那么,通过电阻R的电流有效值和频率分别为( )
如图所示,理想变压器原、副线圈的匝数比为2:1,电阻R=55.0Ω,原线圈两端接一正弦式交变电流,电压u随时间t变化的规律为u=110$\sqrt{2}$sin20πt(V),时间t的单位是s.那么,通过电阻R的电流有效值和频率分别为( )| A. | 1.0A、20Hz | B. | $\sqrt{2}$A、20Hz | C. | $\sqrt{2}$A、10Hz | D. | 1.0A、10Hz |
 如图,一质量为m的条形磁铁用细线悬挂在天花板上,现将金属圆环从水平位置Ⅰ释放,环经过磁铁到达位置Ⅱ.设环经过磁铁上端和下端附近时细线的张力分别为F1和F2,重力加速度大小为g,则( )
如图,一质量为m的条形磁铁用细线悬挂在天花板上,现将金属圆环从水平位置Ⅰ释放,环经过磁铁到达位置Ⅱ.设环经过磁铁上端和下端附近时细线的张力分别为F1和F2,重力加速度大小为g,则( )| A. | F1>mg,F2>mg | B. | F1<mg,F2<mg | C. | F1>mg,F2<mg | D. | F1<mg,F2>mg |
| A. | 气体的密度、体积和摩尔质量 | |
| B. | 阿伏加德罗常数、气体的摩尔质量和密度 | |
| C. | 阿伏加德罗常数、气体的质量和体积 | |
| D. | 阿伏加德罗常数、气体的摩尔质量和质量 |
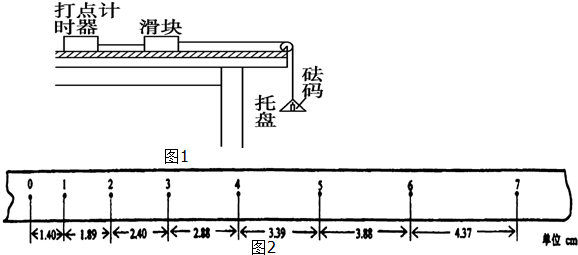
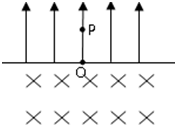 一宇宙人在太空(那里重力可以忽略不计)玩垒球.辽阔的太空球场半侧为均匀电场,场强为E,另半侧为均匀磁场,磁感应强度为B,电场和磁场的分界面为平面,电场方向与界面垂直,磁场方向垂直纸面向里.宇宙人位于电场一侧的P点,O点是P点至界面垂线的垂足,如图所示,现有三个质量相等的垒球,其中垒球1号与垒球2号带电量相同(带负电),垒球3号不带电.且宇宙人每次都是从同一点P投出垒球.宇宙人先在P点由静止释放垒球1号,间隔时间T后以一定初速度v1水平向左抛出垒球2号,垒球2号第一次到达界面时刚好与第二次到达界面的垒球1号相碰.
一宇宙人在太空(那里重力可以忽略不计)玩垒球.辽阔的太空球场半侧为均匀电场,场强为E,另半侧为均匀磁场,磁感应强度为B,电场和磁场的分界面为平面,电场方向与界面垂直,磁场方向垂直纸面向里.宇宙人位于电场一侧的P点,O点是P点至界面垂线的垂足,如图所示,现有三个质量相等的垒球,其中垒球1号与垒球2号带电量相同(带负电),垒球3号不带电.且宇宙人每次都是从同一点P投出垒球.宇宙人先在P点由静止释放垒球1号,间隔时间T后以一定初速度v1水平向左抛出垒球2号,垒球2号第一次到达界面时刚好与第二次到达界面的垒球1号相碰.