题目内容
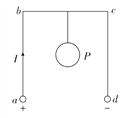
【题目】如图所示,一倾角为60°的光滑斜面固定于水平地面上,Q为斜面顶点,P为斜面上一点,同一竖直平面内有固定点O,O、P连线垂直于斜面,OP=l,P、Q间距离xPQ=![]() l。长度为l的轻绳一端系于O点,另一端系质量为m的小球A,质量为M=4m的滑块B在一锁定装置作用下静止于斜面上的P点。现将A球拉至与O点等高的水平位置,拉直轻绳,以竖直向下的初速度v0释放,A与B发生碰撞前一瞬间,锁定装置解除,A、B均视为质点,碰撞过程中无能量损失,重力加速度为g。
l。长度为l的轻绳一端系于O点,另一端系质量为m的小球A,质量为M=4m的滑块B在一锁定装置作用下静止于斜面上的P点。现将A球拉至与O点等高的水平位置,拉直轻绳,以竖直向下的初速度v0释放,A与B发生碰撞前一瞬间,锁定装置解除,A、B均视为质点,碰撞过程中无能量损失,重力加速度为g。

(1)求小球A通过最低点C点时,绳对小球拉力的大小;
(2)求小球A与滑块B碰撞后瞬间,小球A和滑块B的速度vA和vB
(3)若A、B碰后,滑块B能沿斜面上滑越过Q点,且小球A在运动过程中始终不脱离圆轨道,求初速度v0的取值范围。
【答案】(1) ![]() (2)
(2) ![]() ,
, ![]() (3)
(3) ![]() 或
或![]()
【解析】(1)小球A摆到C点时,设速度为vC,绳对小球的拉力大小为T,则![]()
![]()
在C点,对小球A,由牛顿第二定律有: ![]()
解得: ![]()
![]()
(2)设小球A在与B碰前的速度为v1![]() ,则
,则![]()
对于碰撞过程,取沿斜面向上为正方向,由动量守恒定律得mv1=mvA+MvB
由机械能守恒定律有: ![]()
解得: ![]() ,
, ![]() ,
, ![]()
(3)讨论:①滑块B能沿斜面上滑越过Q点,则![]()
![]()
解得: ![]()
②小球A不能做完整圆周运动,但不脱离圆轨道,即回到最右端位置时速度不能大于零,
则: ![]()
解得: ![]()
③小球A能做完整圆周运动,即能够过最高点,设小球A恰能过最高点的速度为v2![]() ,
,
则: ![]()
![]()
小球A能过圆轨道的最高点的条件为: ![]()
解得: ![]()
![]()
初速度![]() v0的取值范围:
v0的取值范围: ![]() 或
或![]()

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目