题目内容
如图(甲)所示,在场强大小为E、方向竖直向上的匀强电场中存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强方向向右的正电荷,电荷的质量为m、电量为q,不计电荷重力、电荷之间的作用力.
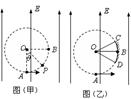
(1)若某电荷的运动轨迹和圆形区域的边缘交于P点,如图(甲)所示,∠POA=θ,求该电荷从A点出发时的速率.
(2)若在圆形区域的边缘有一接收屏CBD,如图(乙)所示,C、D分别为接收屏上最边缘的两点,∠COB=∠BOD=30°.求该屏上接收到的电荷的最大动能和最小动能.

(1)若某电荷的运动轨迹和圆形区域的边缘交于P点,如图(甲)所示,∠POA=θ,求该电荷从A点出发时的速率.
(2)若在圆形区域的边缘有一接收屏CBD,如图(乙)所示,C、D分别为接收屏上最边缘的两点,∠COB=∠BOD=30°.求该屏上接收到的电荷的最大动能和最小动能.
(1) (2)
(2)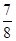 EqR
EqR  EqR
EqR
 (2)
(2)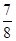 EqR
EqR  EqR
EqR试题分析:(1)a =
 (2分),
(2分),Rsinθ= v0t (1分),
R-Rcosθ=
 at2 (1分),
at2 (1分),由以上三式得v0 =
 (2分)
(2分)(2)由(1)结论得粒子从A点出发时动能为
 m v02 =
m v02 =  (2分)
(2分) 则经过P点时的动能为Ek=Eq(R-Rcosθ)+
 m v02 =
m v02 = EqR (5-3cosθ) (2分)
EqR (5-3cosθ) (2分)可以看出,当θ从0°变化到180°,接收屏上电荷的动能逐渐增大,因此D点接收到的电荷的末动能最小,C点接收到的电荷的末动能最大。
最小动能为:EkD=Eq(R-Rcosθ)+
 m v0D2 =
m v0D2 = EqR (5-3cos60°) =
EqR (5-3cos60°) = 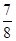 EqR (3分)
EqR (3分)最大动能为:EkC=Eq(R-Rcosθ)+
 m v0C2 =
m v0C2 = EqR (5-3cos120°) =
EqR (5-3cos120°) =  EqR (3分)
EqR (3分)点评:带电粒子在电场中的运动,综合了静电场和力学的知识,分析方法和力学的分析方法基本相同.先分析受力情况再分析运动状态和运动过程(平衡、加速、减速,直 线或曲线),然后选用恰当的规律解题.解决这类问题的基本方法有两种,第一种利用力和运动的观点,选用牛顿第二定律和运动学公式求解;第二种利用能量转化 的观点,选用动能定理和功能关系求解.

练习册系列答案
相关题目



 =45°,已知AO的水平距离为d。(不计重力)求:(1)从A点到B点用的时间;(2)匀强电场的电场强度大小;(3)AB两点间电势差
=45°,已知AO的水平距离为d。(不计重力)求:(1)从A点到B点用的时间;(2)匀强电场的电场强度大小;(3)AB两点间电势差






 =2.8×106m/s的电子,B为金属网,A、B连接在电路上,电源电动势E=20V,内阻不计,滑动变阻器范围为0~20Ω, A、B间距d=10cm,M为荧光屏(足够大),它紧挨着金属网外侧,已知电子的比荷
=2.8×106m/s的电子,B为金属网,A、B连接在电路上,电源电动势E=20V,内阻不计,滑动变阻器范围为0~20Ω, A、B间距d=10cm,M为荧光屏(足够大),它紧挨着金属网外侧,已知电子的比荷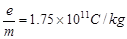 ,现将图中滑动变阻器滑片
,现将图中滑动变阻器滑片
