题目内容
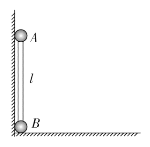
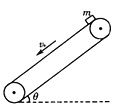
【题目】如图所示,有一条两岸平行,河水均匀流动、流速恒定的大河,河水流速为![]() ,河宽为120m.某人驾着小船渡河,去程时船头朝向始终与河岸垂直,回程时行驶路线最短.已知去程的航线AB与岸边夹角为60°,且船在静水中的速率恒定不变.求:
,河宽为120m.某人驾着小船渡河,去程时船头朝向始终与河岸垂直,回程时行驶路线最短.已知去程的航线AB与岸边夹角为60°,且船在静水中的速率恒定不变.求:
(1)船去程所用时间及渡河路线的总长;
(2)船回程的过程所用时间.

【答案】(1)![]() ;(2)
;(2)![]()
【解析】
将小船的运动分解为沿河岸方向和垂直于河岸方向,根据分运动和合运动具有等时性,依据速度的分解,结合运动学公式,求出垂直于河岸方向上的运动时间,从而求出渡河路线的总长;
当实际航线与河岸垂直,则合速度的方向垂直于河岸,根据平行四边形定则求出船头与河岸所成的夹角,从而求解最小位移所需要的时间。
(1) 由小船去程航线与河岸成60°可知:v船=v水tan60°
渡河时间为:![]()
路线长为:![]() ;
;
(2) 渡河的最小位移即河的宽度.为使船能直达对岸,船头应指向河的上游,并与河岸成一定角度θ
根据三角函数关系有:v船cosθ-v水=0,
![]()
故:![]()
垂直河岸的速度为:v垂=v船sinθ=v船sinθ=![]()
船回程渡河时间为:![]() 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目