题目内容
9. 如图所示,让物体(可视为质点)从图中的C位置由静止开始做圆周运动,其运动轨迹的圆弧与地面相切于最低点D处,物体运动到D点时摆线刚好被拉断,物体在粗糙的水平面上由D点向右做匀减速运动,到达A孔进入半径R=0.36m的竖直放置的光滑圆轨道,当物体进入圆轨道立即关闭A孔.已知摆线长L=2m,θ=60°,物体质量为m=1.0kg,D点与小孔A的水平距离s=2m,g取10m/s2,试求:
如图所示,让物体(可视为质点)从图中的C位置由静止开始做圆周运动,其运动轨迹的圆弧与地面相切于最低点D处,物体运动到D点时摆线刚好被拉断,物体在粗糙的水平面上由D点向右做匀减速运动,到达A孔进入半径R=0.36m的竖直放置的光滑圆轨道,当物体进入圆轨道立即关闭A孔.已知摆线长L=2m,θ=60°,物体质量为m=1.0kg,D点与小孔A的水平距离s=2m,g取10m/s2,试求:(1)摆线所能承受的最大拉力;
(2)要使物体能进入圆轨道并且不脱离轨道,求粗糙水平面摩擦因数μ的范围.
分析 (1)摆球摆到D点时,摆线的拉力最大,根据机械能守恒定律求出摆球摆到D点时速度,由牛顿第二定律求出摆线的最大拉力.
(2)要使摆球能进入圆轨道,并且不脱离轨道,有两种情况:一种在圆心以下做等幅摆动;另一种能通过圆轨道做完整的圆周运动.
小球要刚好运动到A点,对小球从D到A的过程,运用动能定理求出动摩擦因数μ的最大值;
若小球进入A孔的速度较小,并且不脱离轨道,那么将会在圆心以下做等幅摆动,不脱离轨道,其临界情况为到达圆心等高处速度为零,根据机械能守恒和动能定理求出动摩擦因数.
要使摆球能进入圆轨道,恰好到达轨道的最高点,就刚好不脱离轨道,在最高点时,由重力提供向心力,由牛顿第二定律求出此时小球的速度,对从D到轨道最高点的过程,运用动能定理求解动摩擦因数的最小值,即可得到μ的范围
解答 解:(1)当摆球由C到D运动,机械能守恒,则得:mg(L-Lcosθ)=$\frac{1}{2}{mv}_{D}^{2}$
在D点,由牛顿第二定律可得:Fm-mg=$\frac{{mv}_{D}^{2}}{L}$
联立可得:摆线的最大拉力为 Fm=2mg=20N
(2)小球不脱圆轨道分两种情况:
①要保证小球能达到A孔,设小球到达A孔的速度恰好为零,
对小球从D到A的过程,由动能定理可得:-μ1mgs=0-$\frac{1}{2}{mv}_{D}^{2}$
解得:μ1=0.5
若进入A孔的速度较小,那么将会在圆心以下做等幅摆动,不脱离轨道.其临界情况为到达圆心等高处速度为零,由机械能守恒可得:$\frac{1}{2}{mv}_{A}^{2}$=mgR
由动能定理可得:-μ2mgs=$\frac{1}{2}{mv}_{A}^{2}-\frac{1}{2}{mv}_{D}^{2}$
解得:μ2=0.32
②若小球能过圆轨道的最高点则不会脱离轨道,在圆周的最高点由牛顿第二定律可得:$mg-\frac{m{v}^{2}}{R}$
由动能定理可得:$-{μ}_{3}mgs-2mgR=\frac{1}{2}m{v}^{2}-\frac{1}{2}{mv}_{D}^{2}$
解得:μ3=0.05
综上,所以摩擦因数μ的范围为:0.35≤μ≤0.5或者μ≤0.125
答:(1)摆线能承受的最大拉力为20N;
(2)粗糙水平面摩擦因数μ的范围为:0.32≤μ≤0.5或者μ≤0.05
点评 本题关键是不能漏解,要知道摆球能进入圆轨道不脱离轨道,有两种情况,再根据牛顿第二定律、机械能守恒和动能定理结合进行求解

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 子弹以790m/s的速度击中目标 | |
| B. | 汽车通过站牌时的速度是72km/h | |
| C. | 信号沿动物神经传播的速度大约为100m/s | |
| D. | 在市区某段对汽车限速,不得超过60km/h | |
| E. | 台风以36m/s的速度向东北方向移动 |
| A. | 自动报警器 | B. | 电子台秤 | C. | 电视遥控器 | D. | 红外线探测仪 |
 如图所示,一名骑独轮车的杂技演员在空中钢丝绳上表演,如果演员和独轮车的总质量为80kg,两侧的钢丝绳互成120°夹角,则钢丝绳的张力大小为(不计钢丝绳的重力,取g=10m/s2)( )
如图所示,一名骑独轮车的杂技演员在空中钢丝绳上表演,如果演员和独轮车的总质量为80kg,两侧的钢丝绳互成120°夹角,则钢丝绳的张力大小为(不计钢丝绳的重力,取g=10m/s2)( )| A. | 400N | B. | 600N | C. | 800N | D. | 1 600N |
| A. | 衣服受重力、筒壁的弹力和摩擦力、离心力的作用 | |
| B. | 衣服随筒壁做圆周运动的向心力由筒壁的弹力提供 | |
| C. | 筒壁对衣服的摩擦力随着转速的增大而增大 | |
| D. | 筒壁对衣服的弹力随着衣服含水量的减少而增加 |
 如图:物体m由静止开始沿倾角为α的光滑斜面下滑.已知斜面高为H,求
如图:物体m由静止开始沿倾角为α的光滑斜面下滑.已知斜面高为H,求 如图所示为电流天平,可以用来测量匀强磁场的磁感应强度,它的右臂挂着矩形线圈,匝数为n,线圈的水平边长为L,处于匀强磁场内,匀强磁场的方向与线圈平面垂直.当线圈中通过电流I时,调节砝码使两臂达到平衡,然后使电流反向,大小不变,这时需要在左盘中增加质量为m的砝码,才能使两臂再达到新的平衡.
如图所示为电流天平,可以用来测量匀强磁场的磁感应强度,它的右臂挂着矩形线圈,匝数为n,线圈的水平边长为L,处于匀强磁场内,匀强磁场的方向与线圈平面垂直.当线圈中通过电流I时,调节砝码使两臂达到平衡,然后使电流反向,大小不变,这时需要在左盘中增加质量为m的砝码,才能使两臂再达到新的平衡.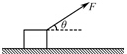 质量m=0.78kg的木块静止于水平面上,现在恒力F作用下做匀加速直线运动,已知恒力大小F=4.5N,方向与水平方向成θ=37°角斜向上,如图所示.3s末撤去此拉力时,木块已滑行的距离s0=9m,(重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.)求:
质量m=0.78kg的木块静止于水平面上,现在恒力F作用下做匀加速直线运动,已知恒力大小F=4.5N,方向与水平方向成θ=37°角斜向上,如图所示.3s末撤去此拉力时,木块已滑行的距离s0=9m,(重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.)求: 如图所示,在匀强电场中有一个等边三角形ABC,且电场线平行于该三角形的平面已知图片里的三点电势(A点电势10V,B点电势2V,C点电势4V)用作图法在图中画出过C点的等势面和过A的电场线.
如图所示,在匀强电场中有一个等边三角形ABC,且电场线平行于该三角形的平面已知图片里的三点电势(A点电势10V,B点电势2V,C点电势4V)用作图法在图中画出过C点的等势面和过A的电场线.