题目内容
（12分）如图所示，在竖直向上磁感强度为B的匀强磁场中，放置着一个宽度为L的金属框架，框架的右端接有电阻R．一根质量为m，电阻忽略不计的金属棒受到外力冲击后，以速度v沿框架向左运动．已知棒与框架间的摩擦系数为μ，在整个运动过程中，通过电阻R的电量为q，设框架足够长．求：
（1）棒运动的最大距离；
（2）电阻R上产生的热量。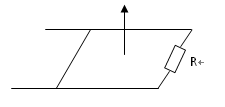
（1）棒运动的最大距离；（2）电阻R上产生的热量。
（1）s=
（2）Q=E电=
mv2-μ
（2）Q=E电=mv2-μ（1）设在整个运动过程中，棒运动的最大距离为s，ΔΦ=BLs，
又q=
Δt=
=
，
由这几式可求出棒运动的最大距离s=．
（2）在整个运动过程中，金属棒的动能一部分转化为电能，另一部分克服摩擦力做功，根据能量守恒定律有：mv2=E电+μmgs 而电能又以焦耳热的形式消耗，故R上产生的热能为Q=E电=mv2-μ
本题考查法拉第电磁感应定律，由公式q=It可求得通过导体棒的电量，其中I为平均电流，由欧姆定律和法拉第电磁感应定律可知q=，再由磁通量变化量可求得流过导体棒的电量，由此可求得距离大小
又q=
Δt==，由这几式可求出棒运动的最大距离s=
．（2）在整个运动过程中，金属棒的动能一部分转化为电能，另一部分克服摩擦力做功，根据能量守恒定律有：
mv2=E电+μmgs 而电能又以焦耳热的形式消耗，故R上产生的热能为Q=E电=mv2-μ本题考查法拉第电磁感应定律，由公式q=It可求得通过导体棒的电量，其中I为平均电流，由欧姆定律和法拉第电磁感应定律可知q=
，再由磁通量变化量可求得流过导体棒的电量，由此可求得距离大小
练习册系列答案
相关题目
t(V)，则
时，电动势达最大值
