题目内容
某一长直的赛道上,有一辆F1赛车前方200m处有一安全车正以10m/s的速度匀速前进,这时赛车从静止出发以2m/s2的加速度追赶.试求:
(1)赛车出发3s末的瞬时速度大小.
(2)赛车何时追上安全车?
(3)赛车追上安全车之前何时与安全车距离最远?
解:(1)根据v=at得,v=2×3m/s=6m/s.
故赛车出发3s末的瞬时速度大小为6m/s.
(2)赛车追上安全车时有:
解得t=20s
赛车经过20s追上安全车.
(3)当两车速度相等时,两车相距最远.
v0=at′解得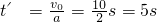 .
.
故经过5s两车相距最远.
分析:(1)根据匀变速直线运动的速度时间公式求出3s末的速度大小.
(2)抓住位移关系,根据运动学公式求出追及的时间.
(3)两车在速度相等前,安全车的速度大于赛车的速度,两者的距离越来越大,速度相等后,赛车的速度大于安全车的速度,两者的距离越来越小.知速度相等时,两车相距最远.
点评:本题属于追及问题,解决的关键是熟练运用运动学公式,知道两车速度相等时,有最大距离.
故赛车出发3s末的瞬时速度大小为6m/s.
(2)赛车追上安全车时有:

解得t=20s
赛车经过20s追上安全车.
(3)当两车速度相等时,两车相距最远.
v0=at′解得
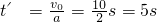 .
.故经过5s两车相距最远.
分析:(1)根据匀变速直线运动的速度时间公式求出3s末的速度大小.
(2)抓住位移关系,根据运动学公式求出追及的时间.
(3)两车在速度相等前,安全车的速度大于赛车的速度,两者的距离越来越大,速度相等后,赛车的速度大于安全车的速度,两者的距离越来越小.知速度相等时,两车相距最远.
点评:本题属于追及问题,解决的关键是熟练运用运动学公式,知道两车速度相等时,有最大距离.

练习册系列答案
相关题目