Question

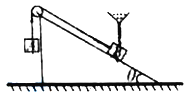
【题目】如图所示，质量M=4kg、高度为h=1.25m的小车放在水平光滑的平面上，质量为m=2kg的小物块位于小车的右端，现给小物块和小车分别向左、向右大小均为v0=3m/s的初速度，物块与小车间的动摩擦因数μ=0.1，当小物块对地位移最大时恰好滑离小车，取g=10m/s2 ． 求：

（1）小车的长度；
（2）小物块滑离小车落地瞬时，小车末端与小物块的水平距离．

Answer 1

【答案】
（1）解：由题可知，当小物块对地位移最大时的速度等于0，小物块与小车组成的系统所受的合外力为零，总动量守恒，取水平向左为正方向，根据动量守恒定律得：

Mv0﹣mv0=Mv+0

解得：v= m/s

根据系统的能量守恒得

μmgL= + ﹣

解得 L=11m

所以为使小物块滑离小车，小车最大长度为3m．

答：小车的长度是11m；

（2）解：小物块滑离小车时水平方向的速度恰好等于0，所以物块与小车分离后做自由落体运动，下落的时间：

t= s．

该过程中小车的位移：

x=vt=1.5×0.5=0.75m

答：小物块滑离小车落地瞬时，小车末端与小物块的水平距离是0.75m．

【解析】本题是物体在小车滑动的类型，根据系统动量守恒和能量守恒，也可以根据牛顿第二定律几运动学基本公式结合求解。
【考点精析】本题主要考查了动量守恒定律的相关知识点，需要掌握动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变才能正确解答此题．