题目内容
2．
如图所示，一根质量不计的轻弹簧上端固定在天花板上，下端与一质量为m的托盘连接，托盘中有一个质量为2m的砝码．当托盘静止时，弹簧的伸长量为L．现将托盘向下拉，弹簧又伸长了L（未超过弹簧的弹性限度），然后使托盘由静止释放，则刚释放托盘时，砝码对托盘的作用力等于（ ）| A． | 3mg | B． | 6mg | C． | 2mg | D． | 4mg |
分析 根据胡克定律求出刚松手时手的拉力，确定盘和物体所受的合力，根据牛顿第二定律求出刚松手时，整体的加速度．再隔离物体研究，用牛顿第二定律求解盘对物体的支持力
解答 解：当盘静止时，由胡克定律得：（m+2m）g=kl…①
设使弹簧再伸长l时手的拉力大小为F，再由胡克定律得：F=kl…②
由①②联立得：F=$\frac{l}{l}$（m+2m）g=3mg
则以盘和物体整体为研究对象，刚松手时所受合力大小等于F，方向竖直向上．
设刚松手时，加速度大小为a，根据牛顿第二定律得：a=$\frac{F}{m+2m}$=g
对物体研究：FN-2mg=2ma
解得：FN=4mg
故选：D
点评 本题考查应用牛顿第二定律分析和解决瞬时问题的能力，这类问题往往先分析平衡状态时物体的受力情况，再分析非平衡状态时物体的受力情况，根据牛顿第二定律求解瞬时加速度
练习册系列答案
名校课堂系列答案
相关题目
12．
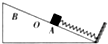如图所示，一轻弹簧一端与挡板固定，另一端自由伸长时位于O点，当另一端和物块相连时，A、B是物块能保持静止的位置中离挡板最近和最远的点．A、B两点离挡板的距离分别为x1、x2．物块与斜面的最大静摩擦力为f，则弹簧的劲度系数为（ ）
如图所示，一轻弹簧一端与挡板固定，另一端自由伸长时位于O点，当另一端和物块相连时，A、B是物块能保持静止的位置中离挡板最近和最远的点．A、B两点离挡板的距离分别为x1、x2．物块与斜面的最大静摩擦力为f，则弹簧的劲度系数为（ ）| A． | $\frac{f}{{x}_{2}+{x}_{1}}$ | B． | $\frac{2f}{{x}_{2}+{x}_{1}}$ | C． | $\frac{f}{{x}_{2}-{x}_{1}}$ | D． | $\frac{2f}{{x}_{2}-{x}_{1}}$ |
10．
如图所示，质量相等的物体A、B通过一轻质弹簧相连，开始时B放在地面上，A、B均处于静止状态，此时弹簧压缩量△x1．现通过细绳将A向上缓慢拉起，第一阶段拉力做功为W1时，弹簧变为原长；第二阶段拉力再做功W2时，B刚要离开地面，此时弹簧伸长量为△x2．弹簧一直在弹性限度内，则（ ）
如图所示，质量相等的物体A、B通过一轻质弹簧相连，开始时B放在地面上，A、B均处于静止状态，此时弹簧压缩量△x1．现通过细绳将A向上缓慢拉起，第一阶段拉力做功为W1时，弹簧变为原长；第二阶段拉力再做功W2时，B刚要离开地面，此时弹簧伸长量为△x2．弹簧一直在弹性限度内，则（ ）| A． | △x1＞△x2 | |
| B． | 拉力做的总功等于A的重力势能的增加量 | |
| C． | 第一阶段，拉力做的功等于A的重力势能的增加量 | |
| D． | 第二阶段，拉力做的功等于A的重力势能的增加量 |
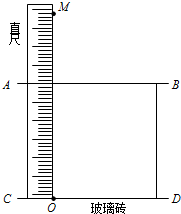现要估测一矩形玻璃砖的折射率n，给定的器材有：待测玻璃砖、白纸、铅笔、大头针1枚、直尺、直角三角板．实验时，先将直尺的一端O和另一点M标上两个明显的标记，再将玻璃砖平放在白纸上，沿其两个长边在白纸上画出两条直线AB、CD，再将直尺正面紧贴玻璃砖的左边缘放置，使O点与直线CD相交，并在白纸上记下点O、点M的位置，如图所示，然后在右上方通过AB所在界面向左下方观察，调整视线方向，直到O点的像与M点的像重合，再在AB直线上插上大头针，使大头针挡住M、O的像，记下大头针P点的位置．
11．
一个质量为0.5kg的物体，从静止开始做直线运动，物体所受合外力F随物体位移x变化的图象如图所示，则物体位移x=8m时速度大小为（ ）
一个质量为0.5kg的物体，从静止开始做直线运动，物体所受合外力F随物体位移x变化的图象如图所示，则物体位移x=8m时速度大小为（ ）| A． | 2m/s | B． | 8m/s | C． | 4$\sqrt{2}$m/s | D． | 4m/s |
12．跳水比赛是我国的传统优势项目，运动员进行10m跳台比赛时，不计空气阻力，在空中运动时下列说法正确的是（ ）
| A． | 为了研究运动员的技术动作，可将正在比赛的运动员视为质点 | |
| B． | 运动员在下落过程中，会感觉到水面在匀加速上升 | |
| C． | 前一半位移用的时间短，后一半位移用的时间长 | |
| D． | 前一半时间内位移大，后一半时间内位移小 |