题目内容
3.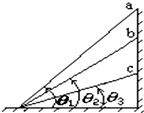 质量为m的物体,分别沿底端到墙壁距离相等、但倾角不同的三个斜面a、b、c从顶端自由滑下,如图所示.三个斜面的倾角θ1>θ2>θ3,物体与三个斜面的动摩擦因数相同.从a、b、c三个斜面顶端滑到底端的过程克服摩擦力做功分别为W1、W2和W3,下到底端时重力的瞬时功率是P1、P2、P3,则( )
质量为m的物体,分别沿底端到墙壁距离相等、但倾角不同的三个斜面a、b、c从顶端自由滑下,如图所示.三个斜面的倾角θ1>θ2>θ3,物体与三个斜面的动摩擦因数相同.从a、b、c三个斜面顶端滑到底端的过程克服摩擦力做功分别为W1、W2和W3,下到底端时重力的瞬时功率是P1、P2、P3,则( )| A. | W1>W2>W3 | B. | P1<P2<P3 | C. | W1=W2=W3 | D. | P1=P2=P3 |
分析 设出斜面的底边长度,利用角度求出斜面长度,由W=FL求的摩擦力做功,利用运动学公式求的时间,即可判断功率.
解答 解:A、C、设斜面底端长为x,则斜面的长度为l=$\frac{x}{cosθ}$
故沿斜面下滑时摩擦力为:f=μmgcosθ
摩擦力做功为:W=fl=μmgx,与倾角无关,故W1=W2=W3,故A错误,C正确.
B、D、物体从斜面顶端滑到底端的过程,由动能定理得:mgh-W=$\frac{1}{2}m{v}^{2}$-0,而竖直方向上的速度v竖=vsinθ.由于斜面a、b、c顶端离地面的高度h1>h2>h3,已知W1=W2=W3,所以v1>v2>v3,由于θ1>θ2>θ3,则v1竖>v2竖>v3竖,所以P1>P2>P3,故BD错误.
故选:C
点评 本题主要考查了功与功率的求法,注意物体在斜面上运动的过程中,摩擦力做的功与斜面的倾角无关.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
13.一辆汽车从静止开始匀加速开出,然后保持匀速运动,最后匀减速运动,直到停止,表给出了不同时刻汽车的速度( )
| 时刻/s | 1.0 | 2.0 | 3.0 | 5.0 | 7.0 | 9.5 | 10.5 |
| 速度/(m•s-1) | 3 | 6 | 9 | 12 | 12 | 9 | 3 |
| A. | 汽车做匀加速运动时,加速度的大小为3 m/s2 | |
| B. | 与匀加速运动时相比,汽车做匀减速运动时速度变化较快 | |
| C. | 汽车做匀加速运动过程中速度的变化量与匀减速运动过程中速度的变化量相同 | |
| D. | 汽车从开出到停止总共经历的时间是11 s |
14.在真空中有两个点电荷,两者的距离保持一定.若把它们各自的电量都增加为原来的3倍,则两电荷的库仑力将增大到原来的( )
| A. | 3倍 | B. | 6倍 | C. | 9倍 | D. | 3倍 |
11.下列说法中正确的是( )
| A. | 跆拳道比赛中研究运动员的动作时,可以把运动员看成质点 | |
| B. | 出租车是按路程的大小来计费的 | |
| C. | 在田径场1500m长跑比赛中,跑完全程的运动员的位移大小为1500m | |
| D. | 高速公路路牌上显示“北京100km”,表示该处到北京的位移大小为100km |
8.作匀加速直线运动的物体,先后经过A、B两点时,其速度分别为v和7v,经历的时间为t,则( )
| A. | 经A、B中点位置时的速度是4v | |
| B. | 从A到B所需时间的中点($\frac{t}{2}$)的速度是4v | |
| C. | AB间的距离为5vt | |
| D. | AB间的距离为4vt |
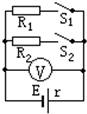 如图所示,电阻R1=14Ω,R2=$\frac{70}{9}$Ω,合上开关S1时,电压表示数为2.8V,当S1、S2都合上时,电压表示数为2.5V,求电源电动势和内阻.
如图所示,电阻R1=14Ω,R2=$\frac{70}{9}$Ω,合上开关S1时,电压表示数为2.8V,当S1、S2都合上时,电压表示数为2.5V,求电源电动势和内阻.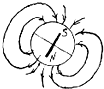 图为地磁场磁感线的示意图,在北半球地磁场的竖直分量向下.飞机在我国上空巡航,机翼保持水平,飞行高度不变.由于地磁场的作用,金属机翼上有电势差.设飞行员左方机翼末端处的电势为φ1,右方机翼末端处的电势为φ2( )
图为地磁场磁感线的示意图,在北半球地磁场的竖直分量向下.飞机在我国上空巡航,机翼保持水平,飞行高度不变.由于地磁场的作用,金属机翼上有电势差.设飞行员左方机翼末端处的电势为φ1,右方机翼末端处的电势为φ2( )