题目内容
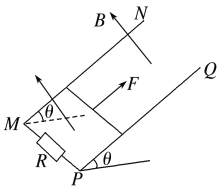
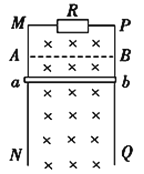
【题目】如图所示，在xOy坐标系中第一象限内存在垂直纸面向里的匀强磁场第二象限内有平行于x轴的有界匀强电场，电场的边界AB、CD均与y轴平行，且OB=BD。一电荷量为+q、质量为m的带电粒子(重力不计)，从P(a，0)点以速度v0垂直射入磁场，其速度方向与x轴成30°夹角，然后从y轴上的N点（图中未画出)垂直于y轴离开磁场，粒子进入第二象限后恰好不穿过CD。已知粒子从第一次通过N点到第二次通过N点所用时间为t0。求：
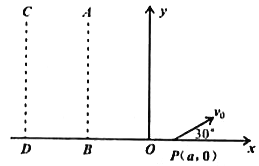
(1)匀强磁场的磁感应强度大小；
(2)带电粒子自P点开始到第一次到达N点所用的时间；
(3)匀强电场的电场强度大小。
【答案】(1)
(2)
(3)
【解析】
（1）利用几何关系求出运动的加速度，则可以求出磁场的磁感应强度B
（2）求出带电粒子在磁场中运动的圆心角，即可求得运动时间。
（3）利用动能定理及运动学公式求出电场强度的大小。
（1）带电粒子运动轨迹及电场方向如图所示
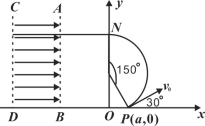
圆周运动半径
根据
匀强磁场的磁感应强度
（2）由周期公式
带电粒子自P点开始到第一次到达N点所用的时间
（3）设粒子从N点向左匀速运动时间为
，位移为x，在电场中匀减速运动时间为
，位移为x
则有 
又
解得： 
粒子从进入电场到匀减速为零，由动能定理得
匀强电场的电场强度
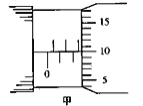
【题目】(1)在“测定金属丝的电阻率”实验中，先用螺旋测微器测出金属丝的直径，测量示数如图甲所示，则金属丝的直径d=________ mm。
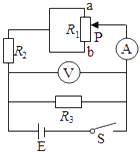
(2)利用电流表和电压表测定一节干电池的电动势和内电阻。要求尽量减小实验误差，实验电路如图所示。
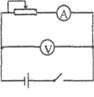
①现有电流表(0-0．6A)、开关和导线若干，以及以下器材：
A．电压表(0~15V) B．电压表(0~3V)
C．滑动变阻器(0~50Ω) D．滑动变阻器(0~500Q)
实验中电压表应选用________；滑动变阻器应选用________。（选填相应器材前的字母）
②某位同学记录的6组数据如下表所示，其中5组数据的对应点已经标在图的坐标纸上，请标出余下的一组数据的对应点，并画出U-I图线________。
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
电压U(V) | 1.45 | 1.40 | 1.30 | 1.25 | 1.20 | 1.10 |
电流I(A) | 0.060 | 0.120 | 0.240 | 0.260 | 0.360 | 0.480 |
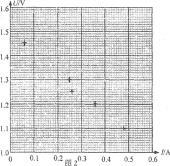
(3)根据(2)中所画图线可得出干电池的电动势E=________V，内电阻r=________Ω，电动势的测量值比真实值________（偏大或偏小），该误差是_______ （系统误差或偶然误差）。
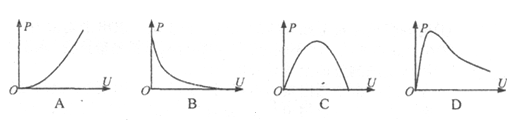
(4)实验中随着滑动变阻器滑片的移动，电压表的示数U及干电池的输出功率P都会发生变化，图各示意图中正确反映P-U关系的是___。
